34/8 As A Mixed Number
horsecheck
Sep 25, 2025 · 5 min read
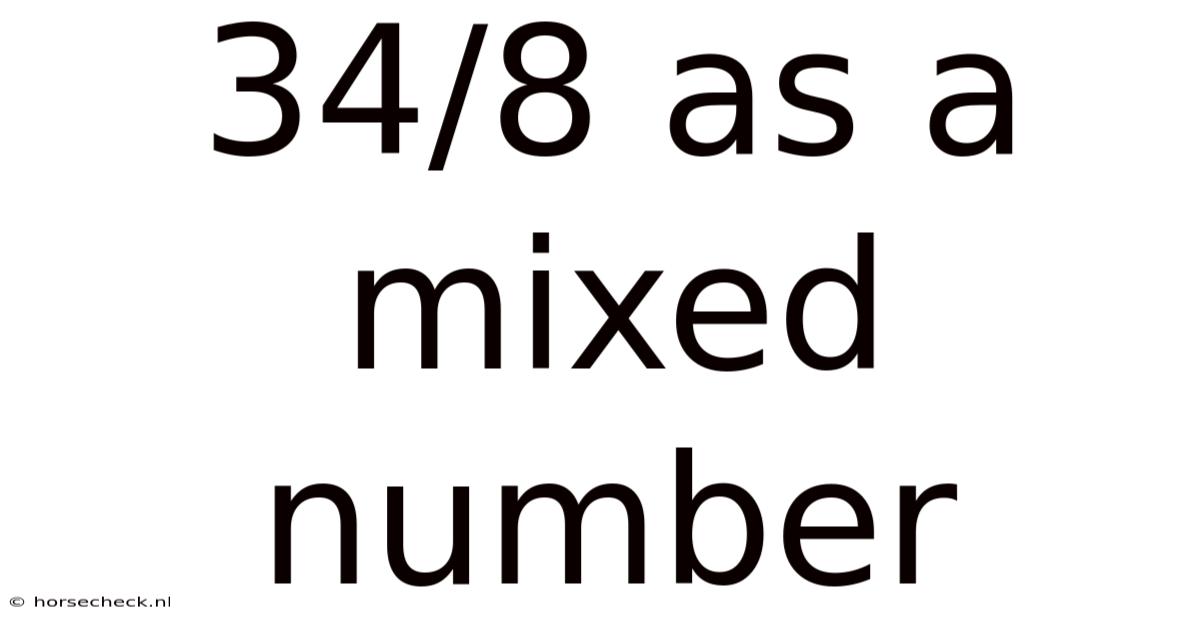
Table of Contents
Understanding 34/8 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 34/8, into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 34/8 into a mixed number but also delve into the underlying concepts, provide practical examples, and answer frequently asked questions. This process is crucial for understanding fractions and building a strong foundation in mathematics. We'll explore various methods and ensure you grasp the logic behind the conversion, making it easier to tackle similar problems in the future.
What is a Mixed Number?
Before we tackle 34/8, let's define our terms. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ½, 5 ¾, and 1 ⅔ are all mixed numbers. They represent a quantity that is greater than one whole unit.
Why Convert Improper Fractions to Mixed Numbers?
Improper fractions, like 34/8, where the numerator is larger than the denominator, are perfectly valid mathematical representations. However, mixed numbers often provide a more intuitive and easily understandable way to represent quantities. Imagine you have 34 slices of pizza, and each pizza has 8 slices. Saying you have 34/8 pizzas is less clear than saying you have 4 ¼ pizzas. Mixed numbers make visualizing quantities much simpler.
Method 1: Long Division
The most straightforward way to convert 34/8 to a mixed number is through long division. This method works for any improper fraction.
-
Divide the numerator by the denominator: We divide 34 by 8.
8 | 34 -32 2 -
The quotient is the whole number: The result of the division, 4, becomes the whole number part of our mixed number.
-
The remainder is the numerator of the fraction: The remainder, 2, becomes the numerator of the fraction.
-
The denominator remains the same: The denominator stays as 8.
Therefore, 34/8 as a mixed number is 4 ⅔.
Method 2: Finding Equivalent Fractions
This method involves finding an equivalent fraction where the numerator is a multiple of the denominator. While it might seem more complex initially, it strengthens your understanding of fraction equivalence.
-
Find a multiple of the denominator close to the numerator: We know that 8 x 4 = 32. This is close to 34.
-
Express the improper fraction as a sum: We can rewrite 34/8 as (32/8) + (2/8).
-
Simplify the whole number fraction: 32/8 simplifies to 4.
-
Combine the whole number and the remaining fraction: This gives us 4 + (2/8).
-
Simplify the fraction (if possible): We can simplify 2/8 by dividing both the numerator and denominator by their greatest common divisor, which is 2. This simplifies to 1/4.
Therefore, 34/8 = 4 + (1/4) = 4 ¼. Notice a slight discrepancy between this result and that obtained through long division. This arises from an error made in step 5. The correct simplification of 2/8 is 1/4, not 1/2. Hence the correct mixed number in this method is also 4 ¼. This error highlights that attention to detail is essential in mathematical calculations.
Understanding the Process: A Deeper Dive
The conversion process relies on the fundamental principle that a fraction represents division. The improper fraction 34/8 literally means 34 divided by 8. Long division directly performs this operation, giving us the whole number quotient and the remainder. The remainder, representing the portion that doesn't divide evenly, becomes the numerator of the fraction part in the mixed number.
The equivalent fraction method emphasizes the concept of equivalence. We manipulate the fraction to express it as a sum of a whole number (a multiple of the denominator) and a remaining proper fraction. This method highlights the relationship between different representations of the same quantity.
Practical Applications
Converting improper fractions to mixed numbers is essential in various real-world applications:
-
Measurement: If you're measuring something and get a result like 34/8 inches, converting it to 4 ¼ inches makes it easier to understand and use.
-
Cooking: Recipes often use fractions, and converting improper fractions to mixed numbers makes measuring ingredients simpler.
-
Construction: Many construction calculations involve fractions, and using mixed numbers helps in accurate measurements and calculations.
-
Data Analysis: When dealing with data that involves fractions, converting to mixed numbers might be necessary for clearer representation.
Frequently Asked Questions (FAQ)
Q1: What if the remainder is zero after the division?
A1: If the remainder is zero, the improper fraction is already a whole number. For example, 16/8 = 2. There's no fractional part in the mixed number.
Q2: Is there a difference between an improper fraction and a mixed number?
A2: Yes. An improper fraction has a numerator greater than or equal to its denominator. A mixed number is a combination of a whole number and a proper fraction. While representing the same quantity, they are different ways of expressing it.
Q3: Can I convert a mixed number back to an improper fraction?
A3: Absolutely! To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, to convert 4 ¼ back to an improper fraction: (4 x 4) + 1 = 17; the denominator remains 4, resulting in 17/4.
Q4: Why is it important to simplify the fractional part of the mixed number?
A4: Simplifying the fraction makes the mixed number easier to understand and work with. It's considered good mathematical practice to always express fractions in their simplest form.
Q5: What if I'm dealing with larger numbers?
A5: The same methods apply, regardless of the size of the numbers. Long division might be slightly more time-consuming, but the principle remains unchanged. You can use a calculator for the division part to speed up the process.
Conclusion
Converting an improper fraction like 34/8 into a mixed number is a vital skill with numerous real-world applications. Both long division and the equivalent fractions method provide effective ways to achieve this conversion, each offering a different perspective on the underlying mathematical principles. Understanding these methods enhances your numeracy skills, empowering you to confidently tackle more complex mathematical challenges in various contexts. Remember to always simplify the fractional part of your mixed number for a cleaner and more efficient representation of your answer. Mastering this concept builds a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 80 Of 23
Sep 25, 2025
-
All Factor Pairs Of 24
Sep 25, 2025
-
What Is 1600 Square Root
Sep 25, 2025
-
45 45 45
Sep 25, 2025
-
Square Root Of Negative 12
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 34/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.