5 6 2 3 Equals
horsecheck
Sep 22, 2025 · 5 min read
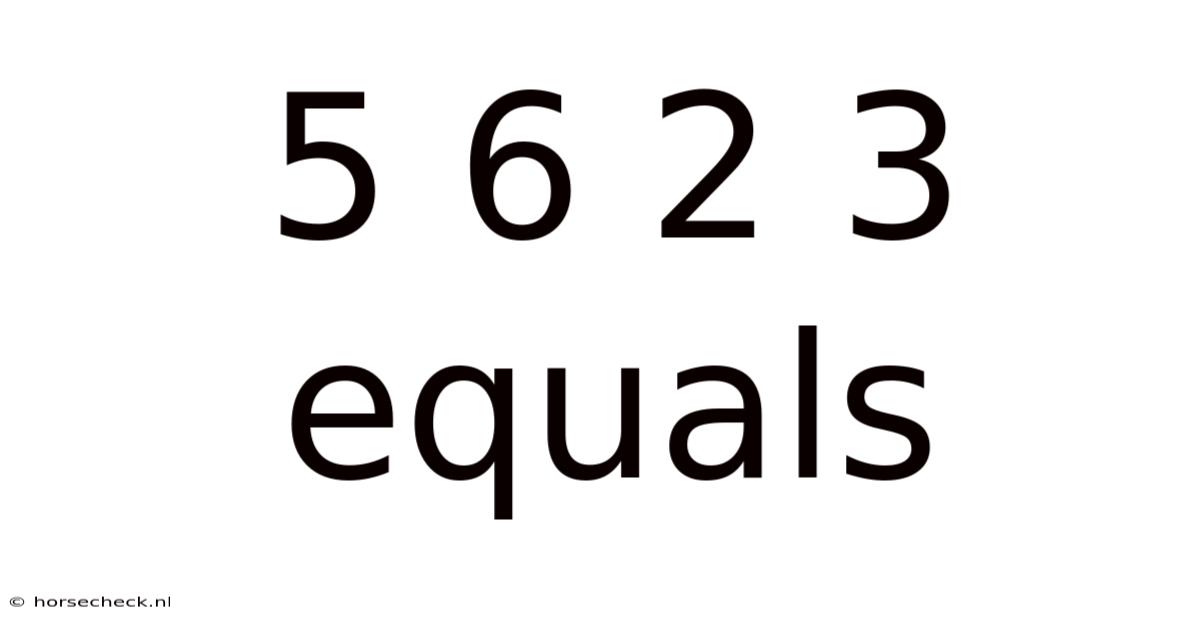
Table of Contents
Decoding "5 6 2 3 Equals": Unveiling the Mystery Behind Mathematical Puzzles
Are you intrigued by mathematical puzzles? Do cryptic sequences like "5 6 2 3 equals" leave you scratching your head, wanting to decipher the hidden logic? This article delves into the fascinating world of numerical puzzles, exploring various techniques and strategies to solve seemingly impossible equations. We'll explore the potential solutions to "5 6 2 3 equals," demonstrating how seemingly simple number sequences can harbor complex, multi-layered solutions. Understanding these techniques will not only help you solve this specific puzzle, but also equip you with the skills to tackle similar mathematical brain teasers.
Understanding the Nature of the Puzzle
The puzzle "5 6 2 3 equals" doesn't represent a standard mathematical equation. There's no single, universally accepted answer. The beauty lies in the ambiguity – it invites us to explore different mathematical operations and patterns to find a logical interpretation that leads to a solution. This type of puzzle requires lateral thinking and a willingness to experiment with different approaches. It tests not just your arithmetic skills but also your problem-solving abilities and creativity.
Potential Solution Approaches: Exploring Different Mathematical Operations
The key to solving this type of puzzle lies in identifying the underlying pattern or rule governing the sequence. Let's explore several potential approaches:
1. Addition, Subtraction, Multiplication, and Division: The Basics
The simplest approach is to explore basic arithmetic operations. However, directly applying addition, subtraction, multiplication, or division to the sequence 5, 6, 2, 3 in a straightforward manner is unlikely to yield a meaningful result. We need to consider more complex combinations or explore other patterns.
2. Sequence-Based Patterns: Identifying Underlying Rules
Perhaps the sequence follows a specific pattern. Let's examine potential rules:
- Differences between consecutive numbers: Calculate the differences between consecutive numbers in the sequence: 6-5=1, 2-6=-4, 3-2=1. This doesn't immediately reveal a consistent pattern.
- Alternating operations: Could we be alternating between addition and subtraction, or multiplication and division? For example, 5 + 6 = 11, then 11 - 2 = 9, then 9 ÷ 3 = 3. This yields a result of 3. However, without knowing the 'equals' value in advance, identifying whether such an alternating pattern is intentional is not definitive.
3. Hidden Mathematical Functions: Going Beyond the Basics
The puzzle might involve more advanced mathematical operations or functions. For instance:
- Exponents and Roots: Could exponents or roots play a role? For example, 5² (25) - 6 = 19, then 19 + 2 = 21, then 21/3 =7.
- Factorials: Factorials (!), which represent the product of all positive integers up to a given number, could be involved. However, using factorials directly in this sequence does not show immediate clear results.
4. Combinations and Permutations: Exploring All Possibilities
We could explore different combinations and permutations of the numbers and operations. This is a more exhaustive approach, but it's computationally intensive and may not guarantee a solution. Let's try a simple example: (5 + 6) * (2 -3) = 11 * (-1) = -11. Again, this demonstrates the absence of a simple, directly apparent solution.
5. Lateral Thinking: Considering Non-Standard Interpretations
This type of puzzle often requires lateral thinking. Could the sequence represent something other than a direct mathematical calculation?
- Number System Conversions: The sequence could represent numbers in a different number system (e.g., binary, hexadecimal). However, without additional clues, converting these decimal numbers doesn't lead to an obvious solution.
- Cipher or Code: Could the numbers be part of a cipher or code that needs to be deciphered? This requires more information or context.
The Importance of Context and Additional Clues
The absence of a specified "equals" value makes solving the puzzle challenging. In many instances, solving these types of numerical puzzles hinges on understanding any contextual clues provided. For example, a visual representation of the numbers or additional instructions would significantly alter the problem-solving approach.
Expanding Our Problem-Solving Toolkit
To effectively tackle these kinds of puzzles, it's essential to develop a robust problem-solving methodology:
- Analyze the given information: Carefully examine the numbers and any contextual clues provided.
- Explore various mathematical operations: Don't limit yourself to basic arithmetic. Experiment with advanced operations, functions, and number system conversions.
- Consider different patterns and sequences: Look for repeating patterns, differences, ratios, or other relationships between the numbers.
- Systematically test different approaches: If you have a hypothesis, test it thoroughly. Keep records of your attempts to avoid repeating the same mistakes.
- Embrace lateral thinking: Consider alternative interpretations of the numbers and their relationships. Think outside the box!
- Don't be afraid to make mistakes: Mathematical puzzles often require trial and error. Learn from your mistakes and refine your approach.
Frequently Asked Questions (FAQ)
Q: Is there only one correct answer to this puzzle?
A: No, without an "equals" value or additional context, there's likely no single "correct" answer. The focus is on exploring different problem-solving methods and understanding the underlying logic.
Q: What if I can't find a solution?
A: This is perfectly normal! Some puzzles are extremely challenging. The process of trying different methods is valuable in its own right, enhancing problem-solving skills.
Q: Are these puzzles useful for anything besides entertainment?
A: Yes, these puzzles are excellent tools for developing critical thinking, problem-solving skills, and creativity. They help individuals practice flexible thinking and improve their ability to approach complex tasks in a methodical manner.
Conclusion: The Value of Mathematical Exploration
The puzzle "5 6 2 3 equals" serves as a microcosm of the broader mathematical landscape. It highlights the importance of exploration, experimentation, and creative problem-solving. The absence of a definitive answer is not a flaw but rather a feature, encouraging a deeper engagement with mathematical concepts and promoting the development of essential cognitive skills. While we may not find a single, universally agreed-upon solution to this specific puzzle, the journey of exploration is far more valuable than the destination itself. By engaging with puzzles like this, we enhance our mathematical intuition and refine our problem-solving prowess. The true reward lies not in finding the answer but in mastering the art of finding an answer, and in the process, gaining a deeper appreciation for the beauty and intricacy of mathematics.
Latest Posts
Latest Posts
-
How Many 50s In 1000
Sep 22, 2025
-
Convert 1 8 To A Decimal
Sep 22, 2025
-
12 Degrees Farenheit To Celcius
Sep 22, 2025
-
12 Divided By 1 1 2
Sep 22, 2025
-
8 Qt How Many Pt
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 6 2 3 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.