66 2 3 To Fraction
horsecheck
Sep 22, 2025 · 6 min read
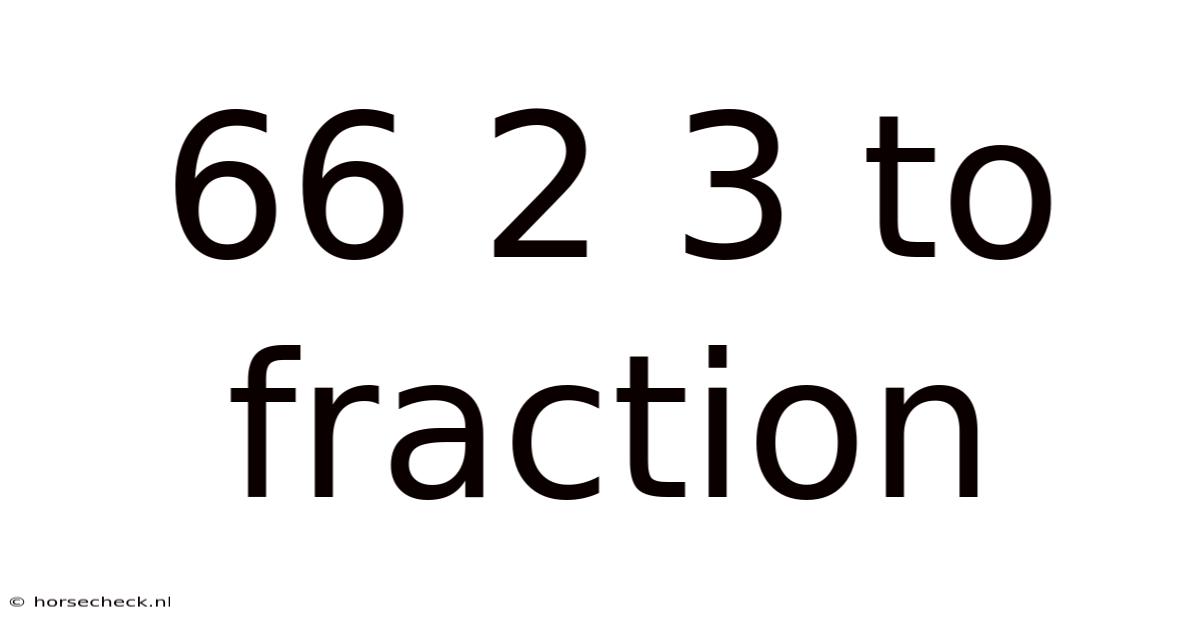
Table of Contents
Decoding the Mystery: Converting 66 2/3 to a Fraction
Many find the conversion of mixed numbers to improper fractions a bit daunting. This article will demystify the process, using the example of 66 2/3, and explore the underlying mathematical principles. We'll break down the steps clearly, providing a thorough understanding, and even tackling some frequently asked questions along the way. By the end, you'll not only know how to convert 66 2/3 to a fraction, but you'll also possess the skills to tackle similar conversions with confidence.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion of 66 2/3, let's establish a firm understanding of the terminology. A mixed number combines a whole number and a fraction, like 66 2/3. An improper fraction, on the other hand, has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). Think of it like having more pieces than a whole would normally have. Converting a mixed number to an improper fraction means expressing the entire quantity as a single fraction.
Step-by-Step Conversion of 66 2/3
Here's how to convert 66 2/3 to an improper fraction:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 66, and the denominator of the fraction is 3. Therefore, we multiply 66 by 3:
66 x 3 = 198
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 2. Adding this to the result from Step 1 (198), we get:
198 + 2 = 200
Step 3: Keep the same denominator.
The denominator of the original fraction remains unchanged. In this case, the denominator is 3.
Step 4: Write the improper fraction.
Combining the results from Steps 2 and 3, we get our improper fraction:
200/3
Therefore, 66 2/3 is equivalent to the improper fraction 200/3.
The Mathematical Rationale Behind the Conversion
The process we just followed isn't just a set of arbitrary steps; it's based on sound mathematical principles. Let's delve deeper:
Imagine you have 66 whole pies, each cut into 3 equal slices. The fraction 2/3 represents two additional slices. To express the total number of slices as a single fraction, we first find the total number of slices from the whole pies. Since each pie has 3 slices, 66 pies would have 66 x 3 = 198 slices. Adding the two extra slices (the numerator of our original fraction), we have a total of 198 + 2 = 200 slices. The denominator remains 3 because each slice represents one-third of a pie. Hence, we arrive at 200/3.
This illustrates the equivalence between the mixed number 66 2/3 and the improper fraction 200/3. They both represent the same quantity.
Practical Applications of Converting Mixed Numbers to Improper Fractions
The ability to convert mixed numbers to improper fractions is crucial in various mathematical contexts. Here are some examples:
-
Adding and Subtracting Fractions: When adding or subtracting fractions with different denominators, it's often easier to work with improper fractions. Converting mixed numbers to improper fractions allows for a more streamlined calculation.
-
Multiplication and Division of Fractions: Similar to addition and subtraction, converting mixed numbers to improper fractions simplifies multiplication and division operations.
-
Solving Algebraic Equations: Many algebraic equations involve fractions, and the ability to convert between mixed numbers and improper fractions is essential for solving them correctly.
-
Real-World Applications: Consider scenarios in cooking (measuring ingredients), construction (calculating materials), or even everyday tasks like sharing items equally. Understanding fraction conversions makes these tasks easier and more accurate.
Beyond 66 2/3: Applying the Conversion Process to Other Mixed Numbers
The method we used to convert 66 2/3 applies to any mixed number. Let's illustrate with another example: Convert 5 1/4 to an improper fraction.
Step 1: 5 x 4 = 20
Step 2: 20 + 1 = 21
Step 3: Denominator remains 4.
Step 4: The improper fraction is 21/4.
This demonstrates the versatility and consistency of the conversion process.
Simplifying Improper Fractions (Optional)
While 200/3 is a perfectly valid improper fraction, sometimes you might want to simplify it further. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 200 and 3 is 1, meaning 200/3 is already in its simplest form. However, if you had an improper fraction like 12/6, you could simplify it to 2/1 or simply 2 by dividing both the numerator and denominator by their GCD (which is 6).
Frequently Asked Questions (FAQ)
Q1: Why do we need to convert mixed numbers to improper fractions?
A1: Converting to improper fractions simplifies arithmetic operations involving fractions, especially addition, subtraction, multiplication, and division. It allows for a more consistent and straightforward approach to calculations.
Q2: Can I convert an improper fraction back to a mixed number?
A2: Absolutely! To convert an improper fraction back to a mixed number, you divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator stays the same. For example, to convert 200/3 back to a mixed number, we divide 200 by 3: 200 ÷ 3 = 66 with a remainder of 2. Therefore, 200/3 = 66 2/3.
Q3: What if the fraction part of the mixed number is already an improper fraction?
A3: That's an interesting case. If you have a mixed number where the fractional part itself is improper (e.g., 2 5/2), you first convert the improper fraction (5/2) to a mixed number (2 1/2). Then, you add this to the whole number part of the original mixed number (2 + 2 1/2 = 4 1/2). Finally, you convert this new mixed number to an improper fraction. In this specific case, 4 1/2 would be (4 x 2 + 1)/2 = 9/2
Q4: Are there any shortcuts for converting mixed numbers to improper fractions?
A4: While the step-by-step method is clearest for understanding the concept, a shortcut involves multiplying the whole number by the denominator, adding the numerator, and keeping the denominator. This can be written concisely as: (Whole number × Denominator + Numerator) / Denominator.
Conclusion
Converting mixed numbers to improper fractions might seem challenging at first, but with a systematic approach and a clear understanding of the underlying mathematical principles, it becomes a straightforward process. We’ve explored the conversion of 66 2/3 in detail, providing a step-by-step guide and addressing common questions. This skill is invaluable in various mathematical applications and real-world scenarios. Mastering this conversion will significantly enhance your mathematical abilities and confidence in tackling fraction-related problems. Remember to practice regularly, and soon you'll be converting mixed numbers to improper fractions with ease.
Latest Posts
Latest Posts
-
4 2 As A Mixed Number
Sep 22, 2025
-
What Numbers Multiply To 48
Sep 22, 2025
-
What Is 25 Of 52
Sep 22, 2025
-
Lcm Of 8 9 10
Sep 22, 2025
-
85 Deg F To C
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 66 2 3 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.