Lcm Of 8 9 10
horsecheck
Sep 22, 2025 · 5 min read
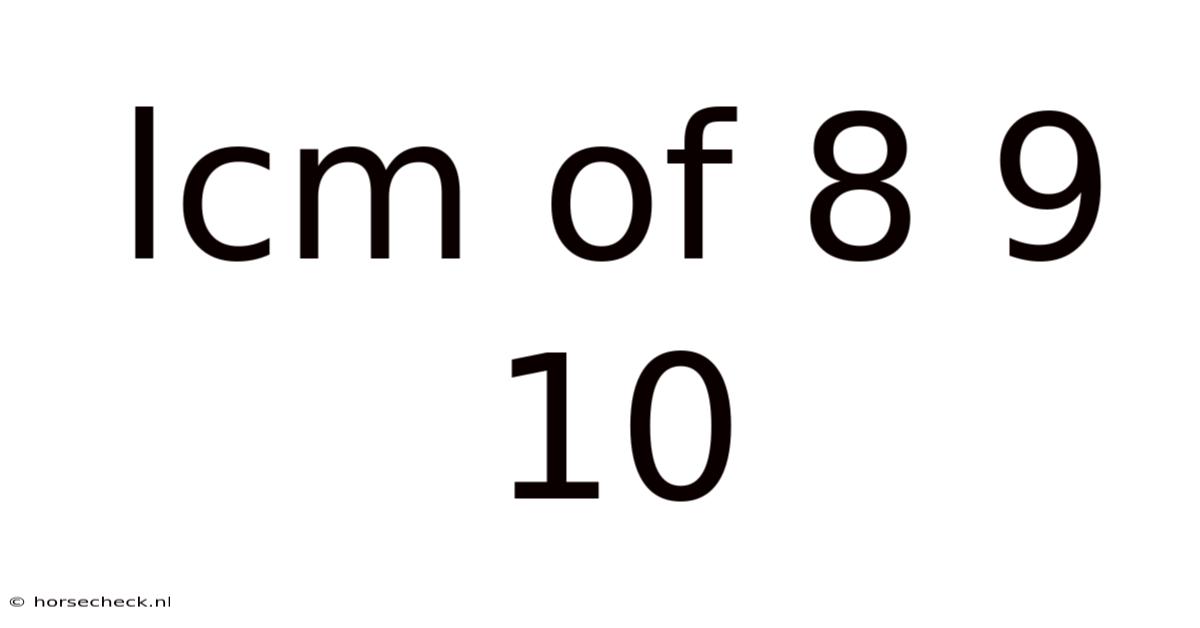
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 9, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications ranging from simple fraction addition to complex scheduling problems. This comprehensive guide will delve into the process of calculating the LCM of 8, 9, and 10, exploring different methods and providing a deep understanding of the underlying principles. We'll cover various approaches, explaining each step in detail and clarifying common misconceptions. By the end, you'll not only know the LCM of 8, 9, and 10 but also possess the skills to calculate the LCM of any set of numbers.
Understanding Least Common Multiple (LCM)
Before we dive into the calculation, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Prime Factorization
This method is considered the most fundamental and reliable way to find the LCM of any set of numbers. It involves breaking down each number into its prime factors. Prime factors are prime numbers (numbers only divisible by 1 and themselves) that multiply together to make the original number.
Steps:
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 9 = 3 x 3 = 3²
- 10 = 2 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(8, 9, 10) = 2³ x 3² x 5 = 8 x 9 x 5 = 360
Therefore, the least common multiple of 8, 9, and 10 is 360. This means 360 is the smallest positive integer that is divisible by 8, 9, and 10 without leaving a remainder.
Method 2: Listing Multiples
This method is simpler for smaller numbers but becomes less efficient as the numbers get larger. It involves listing the multiples of each number until you find the smallest multiple common to all.
Steps:
-
List the multiples of each number:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192, 200, 208, 216, 224, 232, 240, 248, 256, 264, 272, 280, 288, 296, 304, 312, 320, 328, 336, 344, 352, 360...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180, 189, 198, 207, 216, 225, 234, 243, 252, 261, 270, 279, 288, 297, 306, 315, 324, 333, 342, 351, 360...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340, 350, 360...
-
Find the smallest common multiple:
The smallest number that appears in all three lists is 360.
Therefore, the LCM(8, 9, 10) = 360. While this method is straightforward for smaller numbers, it becomes impractical for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b) = (a x b) / GCD(a, b)
This formula can be extended to more than two numbers, but it requires calculating the GCD iteratively. Let's demonstrate this with our example:
Steps:
-
Find the GCD of 8 and 9: The GCD(8, 9) = 1 (they share no common divisors other than 1).
-
Find the LCM of 8 and 9 using the formula: LCM(8, 9) = (8 x 9) / GCD(8, 9) = 72 / 1 = 72
-
Find the GCD of 72 and 10: The GCD(72, 10) = 2
-
Find the LCM of 72 and 10 using the formula: LCM(72, 10) = (72 x 10) / GCD(72, 10) = 720 / 2 = 360
Therefore, the LCM(8, 9, 10) = 360. This method is more efficient than listing multiples for larger numbers, but prime factorization remains generally more efficient and easier to understand for most.
Applications of LCM
The LCM has numerous practical applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling and Timing: Determining when events will coincide, such as the meeting of two buses on different schedules, relies on finding the LCM of their time intervals.
-
Project Management: Coordinating tasks that have different durations often involves using LCM to find the shortest time for all tasks to complete a cycle.
-
Music Theory: Finding the least common multiple of the durations of different musical notes is crucial in music composition and harmony.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder.
-
Q: Can the LCM of two numbers be smaller than both numbers?
- A: No. The LCM will always be greater than or equal to the largest of the given numbers.
-
Q: Is there a formula to calculate the LCM of more than two numbers directly?
- A: While there isn't a single direct formula like the one for two numbers, the prime factorization method works efficiently for any number of integers.
-
Q: What if one of the numbers is zero?
- A: The LCM of any set of numbers including zero is undefined.
Conclusion
Finding the least common multiple is a crucial skill in mathematics with various real-world applications. We've explored three different methods – prime factorization, listing multiples, and using the GCD – to calculate the LCM of 8, 9, and 10, which is 360. The prime factorization method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers. Understanding the concept of LCM and mastering these calculation methods will enhance your mathematical problem-solving abilities significantly. Remember to practice these methods to build confidence and proficiency.
Latest Posts
Latest Posts
-
Lcm For 12 And 36
Sep 22, 2025
-
7 Times What Equals 100
Sep 22, 2025
-
Fun 2nd Grade Math Worksheets
Sep 22, 2025
-
What Is 25 Of 8 00
Sep 22, 2025
-
95 Fahrenheit To Celsius Formula
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 9 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.