7 Times What Equals 100
horsecheck
Sep 22, 2025 · 5 min read
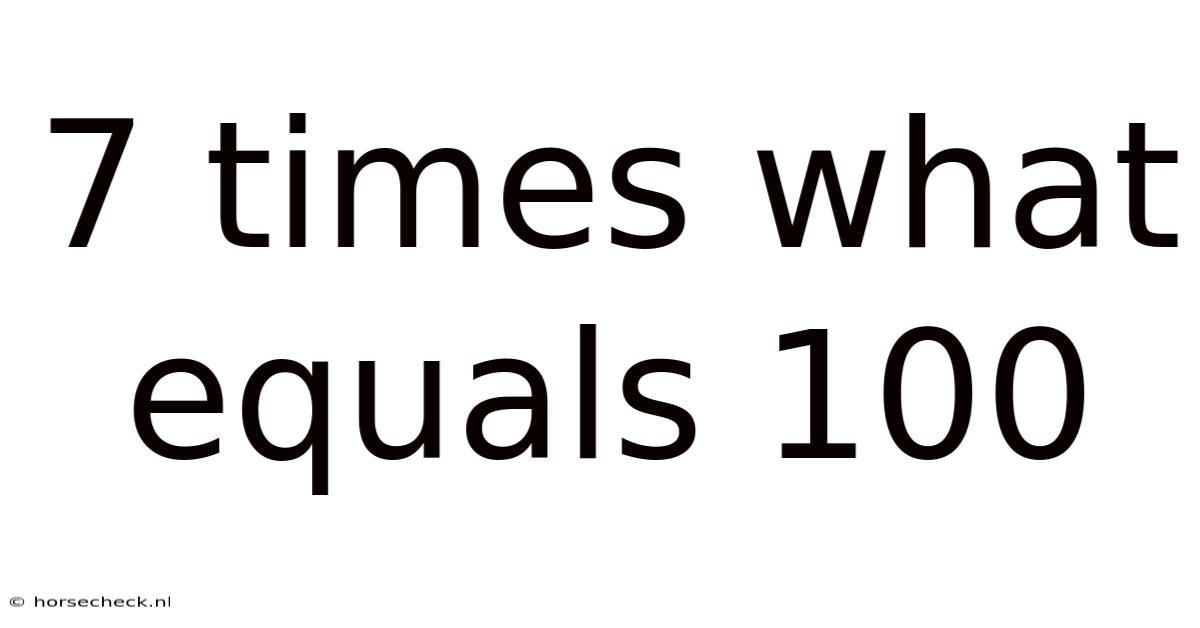
Table of Contents
Decoding the Mystery: 7 Times What Equals 100? A Comprehensive Exploration
Finding the answer to "7 times what equals 100?" might seem like a simple arithmetic problem, easily solved with a quick calculation. However, this seemingly straightforward question opens doors to a deeper understanding of fundamental mathematical concepts, including division, fractions, decimals, and even the application of these concepts in real-world scenarios. This article will not only provide the solution but also delve into the various ways to approach this problem, exploring its implications and highlighting the importance of mathematical literacy.
Introduction: Understanding the Problem
The core question, "7 times what equals 100," is essentially a mathematical equation that can be represented as: 7 * x = 100. Our goal is to find the value of 'x,' the unknown number. This problem utilizes the fundamental concept of multiplication, where we are looking for a multiplier that, when multiplied by 7, results in a product of 100. This seemingly simple equation can be approached using several methods, each providing a deeper insight into the relationship between numbers. Understanding these methods is crucial for building a strong mathematical foundation.
Method 1: Direct Division
The most straightforward approach to solve 7 * x = 100 is to use division. Since multiplication and division are inverse operations, we can isolate 'x' by dividing both sides of the equation by 7:
x = 100 / 7
Performing this division gives us:
x ≈ 14.2857
Therefore, 7 times approximately 14.2857 equals 100. This is an approximate answer because 100 is not perfectly divisible by 7. The result is a decimal number, highlighting the fact that not all multiplication problems result in whole number solutions.
Method 2: Long Division for a Precise Answer
To understand the decimal result more thoroughly, let's explore long division. Long division is a step-by-step method for performing division, particularly useful when dealing with numbers that don't divide evenly.
Here’s how to perform the long division of 100 divided by 7:
- Set up: Arrange the problem as 7)100.
- Divide: 7 goes into 10 one time (7 x 1 = 7). Write the 1 above the 0 in 100.
- Subtract: Subtract 7 from 10, leaving 3.
- Bring down: Bring down the next digit (0) from 100, making it 30.
- Divide: 7 goes into 30 four times (7 x 4 = 28). Write the 4 above the 0 in 100.
- Subtract: Subtract 28 from 30, leaving 2.
- Add a decimal: Add a decimal point to the quotient (14) and add a zero to the remainder (2), making it 20.
- Repeat: Continue the process of dividing, subtracting, and bringing down zeros until you reach the desired level of accuracy or notice a repeating pattern.
This long division process reveals that the quotient is approximately 14.2857, which is a recurring decimal (the digits '2857' repeat infinitely).
Method 3: Fractions – A Precise Representation
Instead of using decimals, we can express the solution as a fraction. The fraction 100/7 represents the exact answer. This fraction is an improper fraction because the numerator (100) is larger than the denominator (7). It can be converted to a mixed number to better understand its value:
100 ÷ 7 = 14 with a remainder of 2.
Therefore, the mixed number representation is 14 2/7. This fraction precisely represents the value of 'x' without any loss of information due to rounding.
Method 4: Applying the Concepts to Real-World Problems
The question "7 times what equals 100" may seem abstract, but its underlying principles have practical applications in various real-world scenarios. For example:
-
Pricing and Quantity: Imagine you're buying items priced at $7 each. To determine how many items you can buy with $100, you'd use this equation. The answer (approximately 14) indicates you can buy 14 items with $100, leaving $2 as change.
-
Resource Allocation: Consider distributing 100 units of a resource equally among 7 teams. Each team would receive approximately 14.29 units (or 14 units with 2 units remaining).
-
Averaging: If 7 individuals collectively earned $100, the average earnings per individual would be approximately $14.29.
These examples demonstrate the relevance of seemingly simple arithmetic problems to everyday life.
Method 5: Using a Calculator
For quick solutions, a calculator is an invaluable tool. Simply input 100 ÷ 7 to get the approximate decimal answer of 14.2857. Calculators are especially helpful when dealing with more complex calculations.
Method 6: Estimation
Before performing any complex calculations, it's useful to estimate the answer. We know that 7 x 10 = 70 and 7 x 20 = 140. Since 100 lies between 70 and 140, we can estimate that the answer will be between 10 and 20, which provides a reasonable range for our solution.
Method 7: Iterative Approximation (Trial and Error)
Another approach is to use trial and error. You can start by multiplying 7 by different numbers until you get close to 100. This method is less efficient for this specific problem but demonstrates a problem-solving approach applicable to situations where precise calculations are difficult or impossible.
Frequently Asked Questions (FAQs)
-
Is there an exact answer? No, there isn't a whole number that, when multiplied by 7, equals 100. The exact answer is the fraction 100/7 or the mixed number 14 2/7.
-
Why is the answer a decimal or fraction? Because 100 is not a multiple of 7; therefore, the division results in a non-whole number.
-
How can I check my answer? Multiply your answer (14.2857 or 100/7) by 7. The result should be approximately 100, acknowledging the inherent rounding in the decimal approximation.
-
What if the question was different? The methods described above can be applied to any similar problem, simply changing the numbers involved.
Conclusion: Mastering the Fundamentals
Solving "7 times what equals 100" extends beyond simply finding the numerical answer. The process reveals the interconnectedness of various mathematical concepts, from division and fractions to real-world applications. Understanding these methods strengthens your mathematical literacy, a skill invaluable in numerous fields and daily life situations. The journey to finding the solution highlights the importance of exploring different approaches and understanding the nuances of mathematical operations. Mastering these fundamental concepts builds a solid base for tackling more advanced mathematical challenges. Remember, mathematics isn't just about memorizing formulas; it's about understanding the underlying principles and their applicability to the real world.
Latest Posts
Latest Posts
-
2 Times What Equals 30
Sep 22, 2025
-
Which Is Equal To 300
Sep 22, 2025
-
11 To The Power Of
Sep 22, 2025
-
What Times What Equals 104
Sep 22, 2025
-
Gcf Of 60 And 40
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 7 Times What Equals 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.