What Times What Equals 104
horsecheck
Sep 22, 2025 · 5 min read
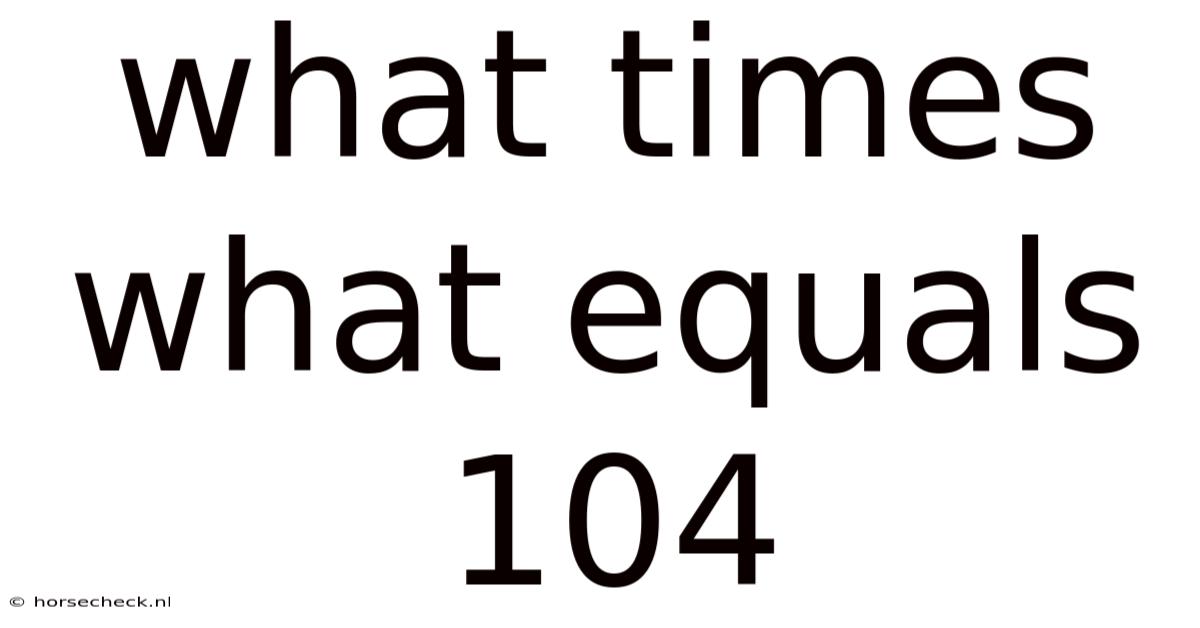
Table of Contents
What Times What Equals 104? Unlocking the Mystery of Factor Pairs
Finding the numbers that multiply to equal 104 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental concepts in mathematics, including factors, prime factorization, and even the beginnings of algebra. This comprehensive guide will not only answer the question "What times what equals 104?" but also equip you with the tools to solve similar problems and appreciate the underlying mathematical principles.
Introduction: Delving into the World of Factors
The core of this problem lies in understanding factors. Factors are numbers that divide evenly into a given number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Finding the factor pairs of 104 involves identifying all the pairs of numbers that, when multiplied together, result in 104.
Finding the Factor Pairs of 104: A Step-by-Step Approach
There are several methods to find the factor pairs of 104. Let's explore some of the most effective approaches:
- Systematic Search: The simplest method involves systematically checking numbers starting from 1. We ask ourselves: "Does 1 divide 104 evenly? What about 2? 3? And so on?"
- 1 x 104 = 104
- 2 x 52 = 104
- 4 x 26 = 104
- 8 x 13 = 104
Once we reach 8, we notice that the next factor, 13, is relatively close. At this point, we've found all the factor pairs. Notice the symmetry; once we find a factor pair, like 2 and 52, we know we've essentially found another pair in reverse order (52 and 2).
- Prime Factorization: A more advanced, but highly efficient method is prime factorization. This involves breaking down the number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's prime factorize 104:
- 104 is an even number, so it's divisible by 2: 104 = 2 x 52
- 52 is also even: 52 = 2 x 26
- 26 is even: 26 = 2 x 13
- 13 is a prime number.
Therefore, the prime factorization of 104 is 2 x 2 x 2 x 13, or 2³ x 13. Using the prime factorization, we can now construct all possible factor pairs by combining different combinations of these prime factors:
- 2¹ x (2² x 13) = 2 x 52
- 2² x (2¹ x 13) = 4 x 26
- 2³ x 13 = 8 x 13
- 1 x (2³ x 13) = 1 x 104
This method guarantees we haven't missed any factor pairs.
Understanding the Mathematical Concepts Involved
Beyond simply finding the answer, let's explore the underlying mathematical principles:
-
Factors and Multiples: Factors are numbers that divide a given number evenly, while multiples are numbers obtained by multiplying a given number by integers (1, 2, 3, and so on). 104 is a multiple of 2, 4, 8, 13, 26, and 52, to name a few.
-
Prime Numbers: Prime numbers are the building blocks of all other numbers. Understanding prime factorization is crucial in number theory and cryptography. The prime factorization of 104 (2³ x 13) shows its fundamental composition.
-
Divisibility Rules: Knowing divisibility rules (e.g., a number is divisible by 2 if it's even, by 3 if the sum of its digits is divisible by 3) can help speed up the process of finding factors.
-
Algebraic Representation: We can represent the problem algebraically. Let's say 'x' and 'y' are the two numbers. Then, the problem becomes: x * y = 104. Solving this equation requires knowing at least one of the variables or having additional information.
Frequently Asked Questions (FAQ)
-
Are there negative factor pairs? Yes! While we typically focus on positive factors, (-1) x (-104) = 104, (-2) x (-52) = 104, and so on. This extends the number of factor pairs considerably.
-
What if the number is very large? For very large numbers, using prime factorization and a computer program becomes highly efficient. Manually testing all numbers would be incredibly time-consuming.
-
What are the applications of finding factor pairs? Factor pairs are fundamental in various mathematical fields, including algebra, number theory, cryptography, and even computer science (in algorithms and data structures).
Advanced Concepts and Extensions
Let's delve into more advanced concepts connected to this seemingly simple problem:
-
Greatest Common Divisor (GCD): The GCD of two numbers is the largest number that divides both numbers evenly. Finding the GCD is essential in simplifying fractions and solving certain algebraic problems. For example, the GCD of 52 and 104 is 52.
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of both numbers. This is useful when working with fractions and finding common denominators. The LCM of 8 and 13 (two factors of 104) is 104.
-
Number Theory: The study of factors, prime numbers, and related concepts forms a significant branch of mathematics called number theory, which has applications in cryptography and computer science.
-
Diophantine Equations: These are equations where only integer solutions are considered. The equation x * y = 104 is a simple example of a Diophantine equation. More complex Diophantine equations are crucial in various areas of mathematics.
Conclusion: More Than Just a Simple Problem
The seemingly simple question, "What times what equals 104?", opens a window into a rich world of mathematical concepts. By exploring the various methods of finding factor pairs, we've touched upon prime factorization, divisibility rules, algebraic representation, and even glimpsed into more advanced areas like number theory and Diophantine equations. This problem serves as a powerful reminder that even seemingly basic arithmetic problems can lead to a deeper appreciation of the elegance and intricacy of mathematics. The journey of exploring the factors of 104 is not just about finding the answer; it’s about understanding the underlying mathematical principles and appreciating the beauty of numbers. This understanding forms a solid foundation for tackling more complex mathematical challenges in the future. Remember, the key is to not just find the answer but also understand the why behind the solution. This approach will transform your understanding of mathematics from rote memorization to a captivating exploration of patterns and logic.
Latest Posts
Latest Posts
-
75 Of 48 Is What
Sep 22, 2025
-
What Is Equal To 6 12
Sep 22, 2025
-
62 5 As A Mixed Number
Sep 22, 2025
-
33 1 3 To Decimal
Sep 22, 2025
-
98 8 Fahrenheit To Celsius
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 104 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.