75 Of 48 Is What
horsecheck
Sep 22, 2025 · 5 min read
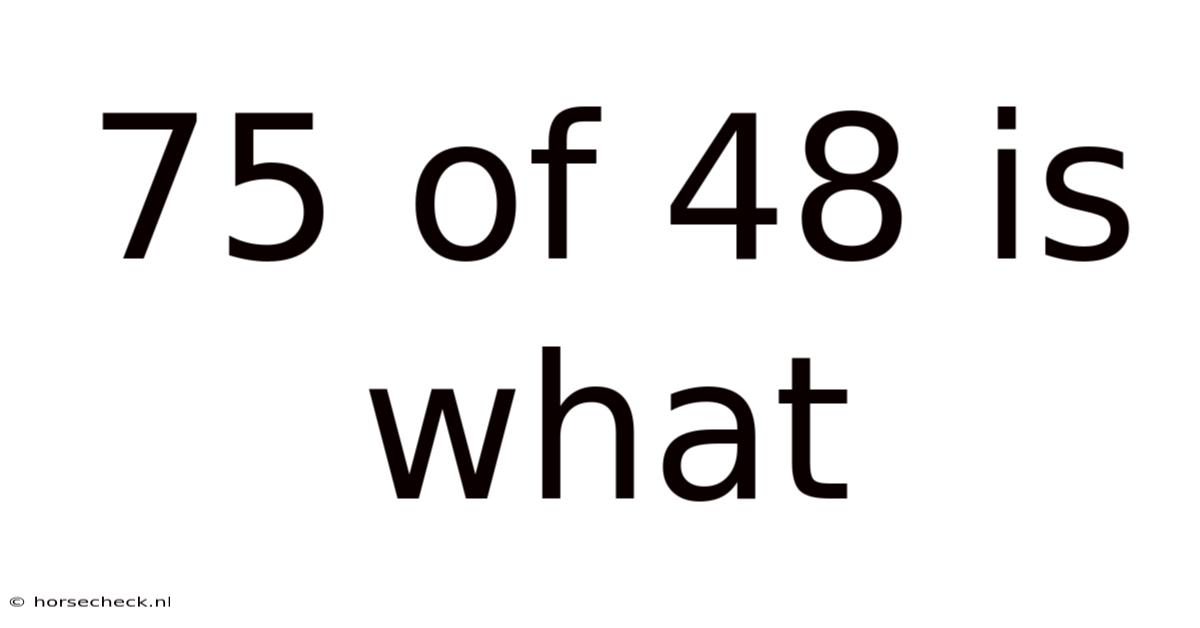
Table of Contents
75 out of 48 is What? Understanding Percentages, Fractions, and Ratios
Finding out what 75 out of 48 represents can seem like a simple math problem, but it opens the door to understanding fundamental mathematical concepts like percentages, fractions, and ratios. This seemingly straightforward question allows us to explore these concepts in depth and apply them to various real-world scenarios. This article will delve into the solution, providing a clear understanding of the process and its broader implications.
Introduction: More Than Just a Simple Calculation
The question, "75 out of 48 is what?" isn't just about getting a numerical answer. It's about understanding the relationship between two numbers and expressing that relationship in different ways. We can interpret this as a fraction (75/48), a ratio (75:48), or a percentage. Each representation offers a unique perspective on the data, making it crucial to understand how to convert between them. This article will guide you through these conversions, exploring the underlying principles and providing practical examples.
Understanding the Basic Concepts
Before we dive into solving "75 out of 48 is what?", let's refresh our understanding of the key mathematical concepts involved:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In our case, 75/48 represents 75 parts out of a total of 48 parts. Notice that the numerator is larger than the denominator, indicating an improper fraction.
-
Ratios: A ratio expresses the relative size of two or more values. The ratio 75:48 indicates the relationship between 75 and 48. It can be simplified by finding the greatest common divisor (GCD) of both numbers.
-
Percentages: A percentage is a fraction expressed as a number out of 100. It is a convenient way to represent proportions and comparisons. To find a percentage, we typically divide the part by the whole and multiply by 100.
Step-by-Step Calculation: Solving 75 out of 48
Let's break down the calculation process to find out what 75 out of 48 represents:
-
Expressing it as a Fraction: The most straightforward representation is the fraction 75/48.
-
Simplifying the Fraction: To simplify 75/48, we find the greatest common divisor (GCD) of 75 and 48. The GCD of 75 and 48 is 3. Dividing both the numerator and denominator by 3, we get 25/16. This simplified fraction still represents the same proportion.
-
Converting to a Mixed Number: Since the numerator is larger than the denominator (25 > 16), we have an improper fraction. We can convert it to a mixed number: 25 divided by 16 is 1 with a remainder of 9. Therefore, 25/16 is equal to 1 9/16. This tells us that 75 out of 48 is equal to one whole and nine-sixteenths more.
-
Converting to a Decimal: To convert the fraction 25/16 to a decimal, we divide 25 by 16: 25 ÷ 16 = 1.5625.
-
Converting to a Percentage: To express this as a percentage, we multiply the decimal by 100: 1.5625 × 100 = 156.25%. This means that 75 is 156.25% of 48. This percentage is greater than 100% because 75 is larger than 48.
Interpreting the Results
The different representations offer varied insights:
-
Fraction (25/16 or 1 9/16): This shows the precise proportional relationship between 75 and 48. It highlights that 75 is more than one and a half times larger than 48.
-
Decimal (1.5625): This provides a concise numerical representation, suitable for calculations and comparisons.
-
Percentage (156.25%): This form is easily understood and readily compared to other percentages. It clearly demonstrates that 75 exceeds 48 by 56.25%.
Real-world Applications
Understanding these calculations has numerous applications:
-
Business and Finance: Analyzing sales figures, comparing profit margins, calculating growth rates. For instance, if 48 units were the sales target and 75 units were sold, the achievement is 156.25% of the target.
-
Science and Engineering: Determining ratios in chemical mixtures, analyzing experimental data, calculating percentages of success rates.
-
Everyday Life: Calculating tips, sharing expenses, understanding discounts, comparing prices.
Advanced Concepts and Extensions
While we've focused on the basic calculations, we can delve deeper into more advanced concepts:
-
Proportions: The equation 75/48 = x/100 represents a proportion, where we solve for x to find the percentage directly. Cross-multiplication provides a convenient method for solving proportions: 75 * 100 = 48 * x. Solving for x gives us x = 156.25.
-
Ratio and Proportion Problems: Many real-world problems involve ratios and proportions. Understanding how to solve these is crucial for many fields.
-
Statistical Analysis: Percentages and ratios are fundamental in statistical analysis, allowing us to analyze data and draw conclusions.
Frequently Asked Questions (FAQ)
-
Q: Why is the percentage greater than 100%?
- A: The percentage is greater than 100% because the numerator (75) is larger than the denominator (48). This signifies that 75 is more than 100% of 48.
-
Q: Can I use a calculator to solve this problem?
- A: Absolutely! Calculators significantly simplify the conversion between fractions, decimals, and percentages.
-
Q: What if the numbers were much larger?
- A: The same principles apply regardless of the size of the numbers. Simplifying fractions might require finding the GCD of larger numbers, which can be done using a calculator or prime factorization.
-
Q: What is the significance of simplifying the fraction?
- A: Simplifying the fraction makes the ratio easier to understand and use in further calculations. It represents the same proportion but in a more concise form.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "75 out of 48 is what?", serves as a gateway to understanding crucial mathematical concepts. By mastering the conversion between fractions, decimals, and percentages, and by applying the principles of ratios and proportions, you equip yourself with skills applicable to a wide range of situations. This comprehensive explanation not only provides the solution but also builds a strong foundation for tackling more complex mathematical challenges. Remember that the key lies in understanding the underlying relationships between numbers and choosing the most appropriate representation for the context. Practice these concepts, and you'll find yourself confidently handling similar problems in the future.
Latest Posts
Latest Posts
-
What Equals 37 In Multiplication
Sep 22, 2025
-
Convert 108 F To C
Sep 22, 2025
-
Square Root Of 24 Simplified
Sep 22, 2025
-
45 Degrees C To Fahrenheit
Sep 22, 2025
-
140 Degrees F In C
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 48 Is What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.