Square Root Of 24 Simplified
horsecheck
Sep 22, 2025 · 6 min read
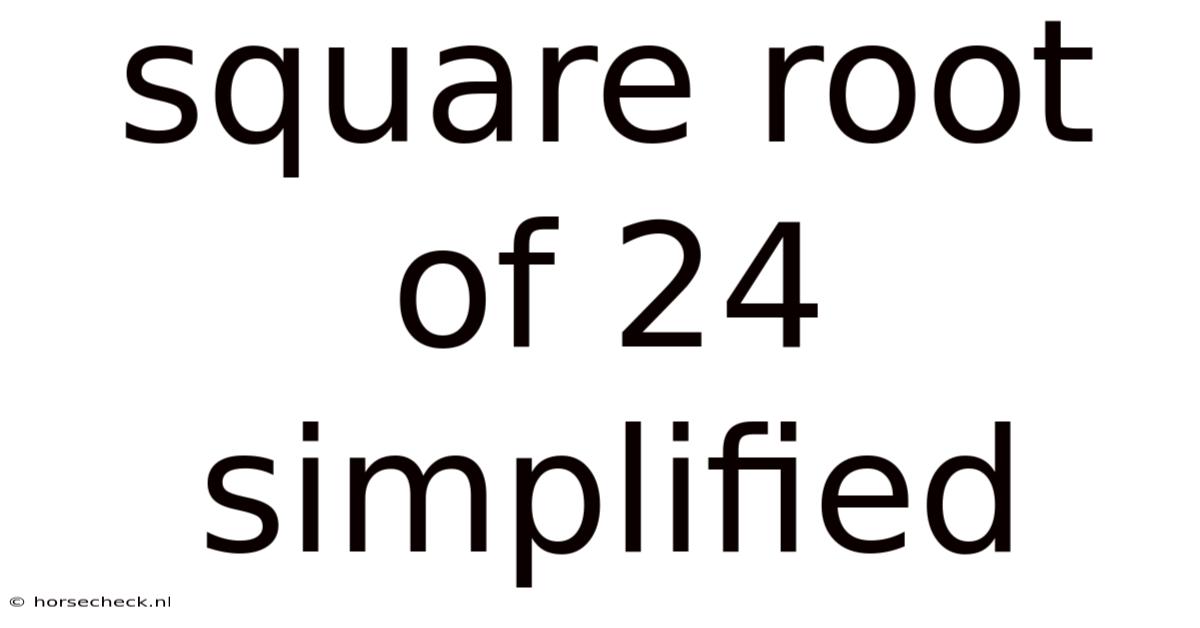
Table of Contents
Unveiling the Mystery: Simplifying the Square Root of 24
Understanding how to simplify square roots is a fundamental concept in mathematics, crucial for various applications from basic algebra to advanced calculus. This article delves deep into the process of simplifying the square root of 24, √24, providing a step-by-step guide, exploring the underlying mathematical principles, and answering frequently asked questions. We'll move beyond a simple answer and explore the broader implications of simplifying radicals. By the end, you'll not only know the simplified form of √24 but also possess a solid understanding of the method and its applications.
Introduction: What Does Simplifying a Square Root Mean?
Simplifying a square root involves expressing it in its simplest form, where no perfect square numbers (other than 1) remain under the radical symbol (√). A perfect square is a number that results from squaring an integer (e.g., 4 is a perfect square because 2 x 2 = 4). The goal is to extract any perfect squares hiding within the radicand (the number under the square root symbol). In essence, we're aiming for a more concise and elegant representation of the root.
Step-by-Step Simplification of √24
Let's break down the simplification of √24 into manageable steps:
-
Find the Prime Factorization: The first crucial step is to find the prime factorization of 24. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). We can represent this as a factor tree:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3
-
Identify Perfect Squares: Now, examine the prime factorization (2³ x 3). Look for pairs of identical prime factors. We have a pair of 2's (2 x 2 = 2²).
-
Extract Perfect Squares: Since 2² is a perfect square, we can remove it from under the radical symbol. Remember, the square root of a perfect square is simply the base number. √(2²) = 2.
-
Simplify the Expression: We're left with one factor of 2 and one factor of 3 still under the radical. Therefore, the simplified expression becomes:
√24 = √(2² x 2 x 3) = 2√(2 x 3) = 2√6
Therefore, the simplified form of √24 is 2√6.
The Mathematical Foundation: Why This Works
The method relies on the fundamental property of square roots: √(a x b) = √a x √b, where 'a' and 'b' are non-negative numbers. This property allows us to break down a complex square root into smaller, more manageable parts. By finding the prime factorization, we effectively break the number down into its fundamental building blocks, making it easier to identify and extract perfect squares. The process is essentially reversing the multiplication inherent in the square root operation.
Beyond √24: Applying the Simplification Technique to Other Radicals
The method demonstrated with √24 is universally applicable to simplifying any square root. Let's consider a few more examples:
-
√72: The prime factorization of 72 is 2³ x 3². This gives us a pair of 2's and a pair of 3's (perfect squares). Therefore, √72 simplifies to 6√2.
-
√125: The prime factorization of 125 is 5³. We have a pair of 5's (5²). Therefore, √125 simplifies to 5√5.
-
√48: The prime factorization of 48 is 2⁴ x 3. We have two pairs of 2's (2² x 2²). Therefore, √48 simplifies to 4√3.
These examples illustrate the versatility and importance of prime factorization in simplifying square roots. It's a systematic approach that works for any number, no matter how large or complex.
Simplifying Square Roots with Variables
The simplification process extends to square roots containing variables. For example, let’s simplify √(18x⁴y³):
-
Prime Factorization: We factorize the numerical coefficient (18) and the variables separately: 18 = 2 x 3²; x⁴ = x² x x²; y³ = y² x y
-
Identify Perfect Squares: We have 3², x², x², and y² as perfect squares.
-
Extract Perfect Squares: This gives us 3, x, x, and y outside the radical.
-
Simplify the Expression: The simplified expression is 3x²y√(2y).
This demonstrates how the same principles apply when dealing with variables, highlighting the importance of understanding exponent rules. Remember that √(x²) = |x| (the absolute value of x) to ensure accuracy for all real numbers.
Applications of Simplifying Square Roots
Simplifying square roots is not just an abstract mathematical exercise. It has practical applications in numerous areas, including:
-
Geometry: Calculating lengths of diagonals in squares, rectangles, or triangles often involves simplifying square roots. For instance, finding the diagonal of a square with side length 'a' involves simplifying √(2a²).
-
Physics: Many physics formulas involve square roots, such as calculations related to speed, velocity, energy, and various other physical phenomena. Simplifying these square roots allows for easier calculations and interpretations of results.
-
Engineering: In engineering design and calculations, square roots frequently appear. Simplifying them improves precision and reduces the complexity of computations.
-
Calculus: Derivative and integral calculations may involve simplifying square roots to obtain more manageable expressions.
Frequently Asked Questions (FAQ)
Q1: What if the number under the square root is a negative number?
A1: The square root of a negative number involves imaginary numbers (represented by 'i', where i² = -1). The simplification process is similar, but the result will include 'i'. For instance, √(-24) = 2i√6.
Q2: Is there a quicker way to simplify square roots than prime factorization?
A2: While prime factorization is the most reliable method, with practice, you might develop an intuition for identifying perfect square factors directly. However, prime factorization guarantees a complete and accurate simplification, especially for larger numbers.
Q3: Can I use a calculator to simplify square roots?
A3: Calculators can provide numerical approximations, but they often don't give the simplified radical form. The simplification process is essential for understanding the mathematical structure and performing further algebraic manipulations.
Q4: What happens if there are no perfect squares in the prime factorization?
A4: If the prime factorization doesn't contain any perfect squares, the square root is already in its simplest form. For example, √17 is already simplified as it contains no perfect square factors.
Conclusion: Mastering the Art of Square Root Simplification
Simplifying square roots, as exemplified by our exploration of √24, is a fundamental skill that extends far beyond rote memorization. It's a testament to the power of prime factorization and the elegance of mathematical principles. By mastering this technique, you'll not only enhance your mathematical proficiency but also gain a deeper appreciation for the underlying structure and beauty of numbers. This article provides a firm foundation for further explorations in algebra and beyond, empowering you to confidently tackle more complex mathematical problems. Remember the steps: prime factorization, identify perfect squares, extract them, and simplify the expression. With practice and understanding, simplifying square roots will become second nature.
Latest Posts
Latest Posts
-
24 As A Prime Factor
Sep 22, 2025
-
98 8 Fahrenheit In Celsius
Sep 22, 2025
-
What Is 85 Of 12
Sep 22, 2025
-
What Is 48 Of 50
Sep 22, 2025
-
Lcm For 16 And 18
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 24 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.