What Is 85 Of 12
horsecheck
Sep 22, 2025 · 5 min read
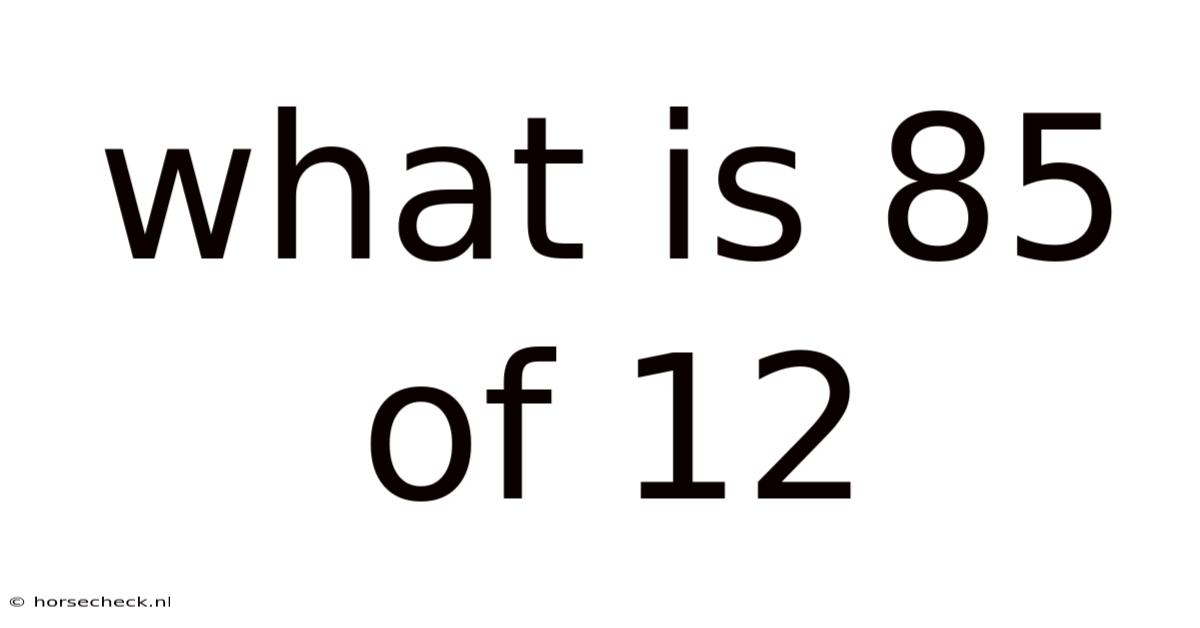
Table of Contents
What is 85% of 12? A Comprehensive Guide to Percentages and Their Applications
Finding 85% of 12 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from everyday budgeting to complex financial analyses. This comprehensive guide will not only answer the question "What is 85% of 12?" but also explore the broader concept of percentages, their practical applications, and different methods for calculating them. We'll delve into the mathematical reasoning behind percentage calculations, offer various solution methods, and even touch upon more advanced percentage-related problems.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). So, 85% means 85 out of 100, or 85/100. This can be expressed as a decimal (0.85) or a fraction (85/100, which simplifies to 17/20). Understanding this fundamental concept is key to solving any percentage problem.
Calculating 85% of 12: Three Methods
There are several ways to calculate 85% of 12. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is often the quickest and most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100.
- Convert the percentage to a decimal: 85% / 100 = 0.85
- Multiply the decimal by the number: 0.85 * 12 = 10.2
Therefore, 85% of 12 is 10.2.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then performing the multiplication.
- Convert the percentage to a fraction: 85% = 85/100
- Simplify the fraction (if possible): 85/100 simplifies to 17/20
- Multiply the fraction by the number: (17/20) * 12 = 204/20
- Simplify the result: 204/20 simplifies to 10.2
Again, we arrive at the answer: 85% of 12 is 10.2.
Method 3: Proportion Method
This method uses proportions to solve the problem. We set up a proportion where we know three of the four values:
- We know the whole (12).
- We know the percentage (85%).
- We want to find the part (x).
The proportion is set up as follows:
85/100 = x/12
To solve for x, we cross-multiply:
100x = 85 * 12 100x = 1020 x = 1020/100 x = 10.2
Therefore, 85% of 12 is 10.2.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses all involve percentages. For example, figuring out the final price after a 20% discount, calculating the interest earned on a savings account, or determining the amount of tax owed on a purchase all require proficiency in percentage calculations.
-
Statistics: Percentages are fundamental to interpreting statistical data. Understanding percentages allows you to analyze survey results, interpret data visualizations like pie charts, and grasp the significance of statistical findings. For example, understanding that 75% of respondents favored a particular product offers valuable market insights.
-
Everyday Life: Percentages are used extensively in daily life. Calculating tips in restaurants, understanding sales and discounts in stores, and even figuring out the nutritional information on food labels all involve percentages. For example, knowing that a cereal contains 10% of your daily recommended fiber intake helps you make informed dietary choices.
-
Science and Engineering: Percentages are used in various scientific and engineering applications, such as expressing concentrations of solutions, calculating efficiency rates of machines, or representing error margins in measurements.
Beyond the Basics: More Complex Percentage Problems
While calculating 85% of 12 is a straightforward example, let's explore some more challenging percentage problems:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For instance, what percentage is 6 of 15? This is solved by dividing the part (6) by the whole (15) and multiplying by 100: (6/15) * 100 = 40%.
-
Finding the Whole: You might know a percentage and the part, but need to find the whole. For example, if 25% of a number is 10, what is the number? This is solved using the equation: (25/100) * x = 10. Solving for x yields x = 40.
-
Percentage Increase/Decrease: Calculating percentage increases or decreases is crucial for tracking changes over time. For example, if a price increases from $10 to $12, the percentage increase is calculated as: [(12-10)/10] * 100 = 20%.
Frequently Asked Questions (FAQ)
Q1: Why is understanding percentages important?
A1: Percentages provide a standardized way to compare and represent proportions. They are crucial for interpreting data, making financial decisions, and understanding various aspects of the world around us.
Q2: Can I use a calculator to calculate percentages?
A2: Yes, most calculators have a percentage function (%) that simplifies the calculation. Simply input the number, press the percentage button, and then multiply by the other number.
Q3: What if I need to calculate a percentage that's not a whole number, like 85.5%?
A3: The same methods apply. Convert 85.5% to its decimal equivalent (0.855) and multiply it by the number.
Q4: Are there any online tools to help with percentage calculations?
A4: Yes, many websites and apps offer percentage calculators that can perform various percentage-related calculations, including finding a percentage of a number, determining percentage increases or decreases, and more.
Q5: How can I improve my skills in percentage calculations?
A5: Practice is key. Start with simple problems and gradually work your way up to more complex scenarios. Using different methods for the same problem can also enhance your understanding and make you more confident in your calculations.
Conclusion
Calculating 85% of 12, which equals 10.2, is a straightforward application of percentage calculations. However, the broader implications of understanding percentages extend far beyond this simple problem. From managing personal finances to interpreting scientific data, a solid grasp of percentages is essential for success in various aspects of life. By mastering different methods of percentage calculation and exploring various applications, you equip yourself with a valuable skill that will serve you well in numerous situations. Remember, consistent practice and a thorough understanding of the underlying principles will significantly improve your proficiency in this crucial mathematical concept.
Latest Posts
Latest Posts
-
4 1 3 Improper Fraction
Sep 23, 2025
-
What Is 50 Of 26
Sep 23, 2025
-
8 5 As Mixed Number
Sep 23, 2025
-
Lcm For 10 And 12
Sep 23, 2025
-
What Is A 20 22 Grade
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 85 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.