79/8 As A Mixed Number
horsecheck
Sep 23, 2025 · 6 min read
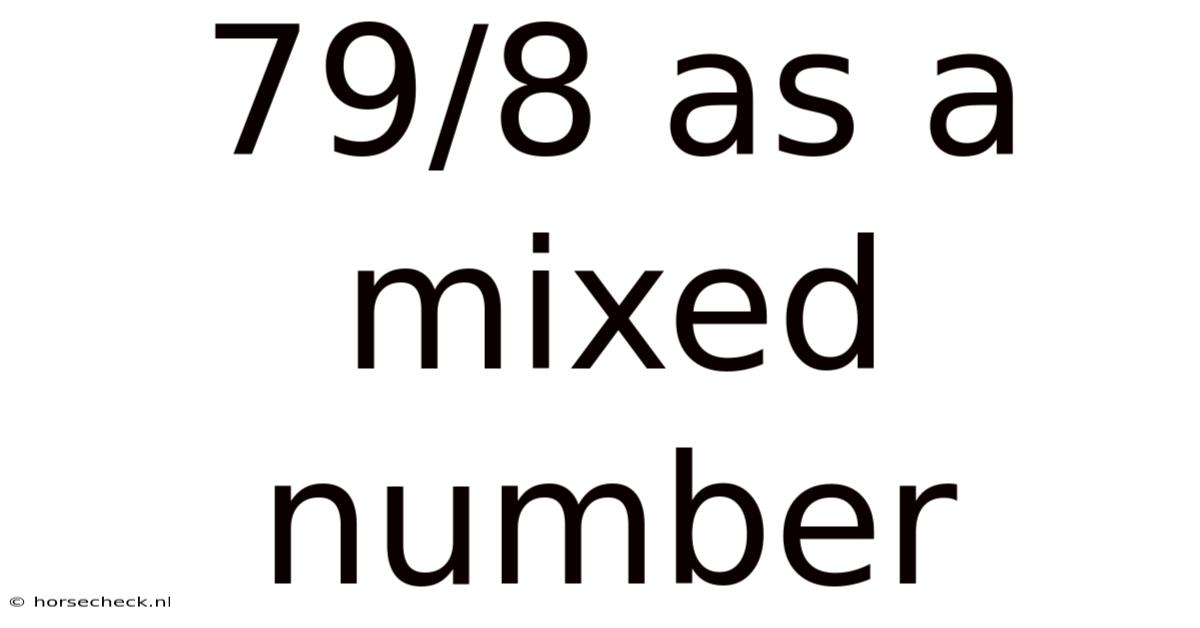
Table of Contents
Decoding 79/8: A Deep Dive into Mixed Numbers
Understanding fractions and converting them into mixed numbers is a fundamental concept in mathematics. This comprehensive guide will walk you through the process of converting the improper fraction 79/8 into a mixed number, explaining the underlying principles and providing practical examples to solidify your understanding. We'll cover the steps involved, explore the underlying mathematical reasons, and address frequently asked questions. This will not only help you solve this specific problem (79/8 as a mixed number) but also equip you with the skills to tackle similar conversions with confidence.
Understanding Fractions and Mixed Numbers
Before we delve into the conversion of 79/8, let's quickly refresh our understanding of fractions and mixed numbers.
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 3/4). Mixed numbers are useful for representing quantities that are greater than one whole unit. For instance, 2 1/2 represents two whole units and one-half of another unit.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4, 8/8, 10/3). Improper fractions are often converted to mixed numbers for easier understanding and use in calculations. This is precisely what we will do with 79/8.
Converting 79/8 to a Mixed Number: A Step-by-Step Guide
Now, let's tackle the conversion of 79/8 into a mixed number. The process involves two main steps: division and interpretation.
Step 1: Divide the Numerator by the Denominator
This is the core of the conversion. We divide the numerator (79) by the denominator (8).
79 ÷ 8 = 9 with a remainder of 7
Step 2: Interpret the Result
The result of the division gives us the components of our mixed number:
- The quotient (9) becomes the whole number part of the mixed number. This represents how many whole units we have.
- The remainder (7) becomes the numerator of the fractional part. This represents the remaining parts of a whole unit.
- The denominator (8) remains the same. This indicates the number of equal parts the whole unit is divided into.
Therefore, 79/8 as a mixed number is 9 7/8.
This means we have nine whole units and seven-eighths of another unit.
Visualizing the Conversion
Imagine you have 79 slices of pizza, and each pizza has 8 slices. To find out how many whole pizzas you have, you divide 79 by 8. You get 9 whole pizzas (9 x 8 = 72 slices). You have 7 slices left over (79 - 72 = 7), which represents 7/8 of another pizza. Therefore, you have 9 7/8 pizzas in total. This visual representation helps solidify the understanding of the mathematical process.
The Mathematical Rationale Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the principle of equivalent fractions. We are essentially expressing the same quantity in a different form. In the case of 79/8, we can break it down as follows:
79/8 = (72 + 7)/8 = 72/8 + 7/8 = 9 + 7/8 = 9 7/8
We decompose the numerator (79) into a multiple of the denominator (72, which is 8 x 9) and the remainder (7). This allows us to separate the whole units from the fractional part, leading to the mixed number representation.
Converting Mixed Numbers Back to Improper Fractions
It's important to understand the reverse process as well. To convert a mixed number back to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 9 x 8 = 72
- Add the numerator: 72 + 7 = 79
- Keep the denominator the same: 8
- The result is the improper fraction: 79/8
This demonstrates the equivalence between the improper fraction and its mixed number representation.
Practical Applications of Mixed Numbers
Mixed numbers are widely used in various real-life scenarios, making their understanding crucial. Some examples include:
- Measurement: Expressing lengths (e.g., 3 1/2 feet), weights (e.g., 2 3/4 pounds), or volumes (e.g., 1 1/2 liters).
- Cooking: Following recipes that require fractional amounts of ingredients.
- Construction: Calculating quantities of materials needed for a project.
- Time: Expressing durations (e.g., 1 1/2 hours).
The ability to easily convert between improper fractions and mixed numbers is essential for accurate calculations and problem-solving in these and many other contexts.
Frequently Asked Questions (FAQ)
Q1: Why do we convert improper fractions to mixed numbers?
A1: While improper fractions are perfectly valid mathematical expressions, mixed numbers are often preferred for their intuitive representation. They offer a clearer picture of the quantity involved, making them easier to understand and use in everyday applications.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, every improper fraction can be converted to a mixed number or a whole number (which is a special case of a mixed number where the fractional part is zero).
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 16/4 = 4. There is no fractional part.
Q4: Are there different methods for converting improper fractions to mixed numbers?
A4: The method described above (division and interpretation) is the most common and straightforward approach. Other methods might exist, but they usually boil down to the same fundamental principle of separating the whole units from the fractional part.
Q5: How can I check if my conversion is correct?
A5: You can always convert the mixed number back to an improper fraction using the steps outlined earlier. If you arrive at the original improper fraction, your conversion is correct.
Conclusion
Converting 79/8 to a mixed number, which results in 9 7/8, is a fundamental skill in mathematics. This process, involving division and interpretation, allows us to represent quantities in a more easily understandable and applicable manner. Understanding the underlying mathematical principles ensures proficiency not only in solving this specific problem but also in handling various similar conversions with confidence. Mastering this skill enhances your abilities in various mathematical contexts and real-world applications. Remember to practice regularly to solidify your understanding and increase your speed and accuracy in converting between improper fractions and mixed numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about 79/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.