Lcm Of 25 And 15
horsecheck
Sep 25, 2025 · 6 min read
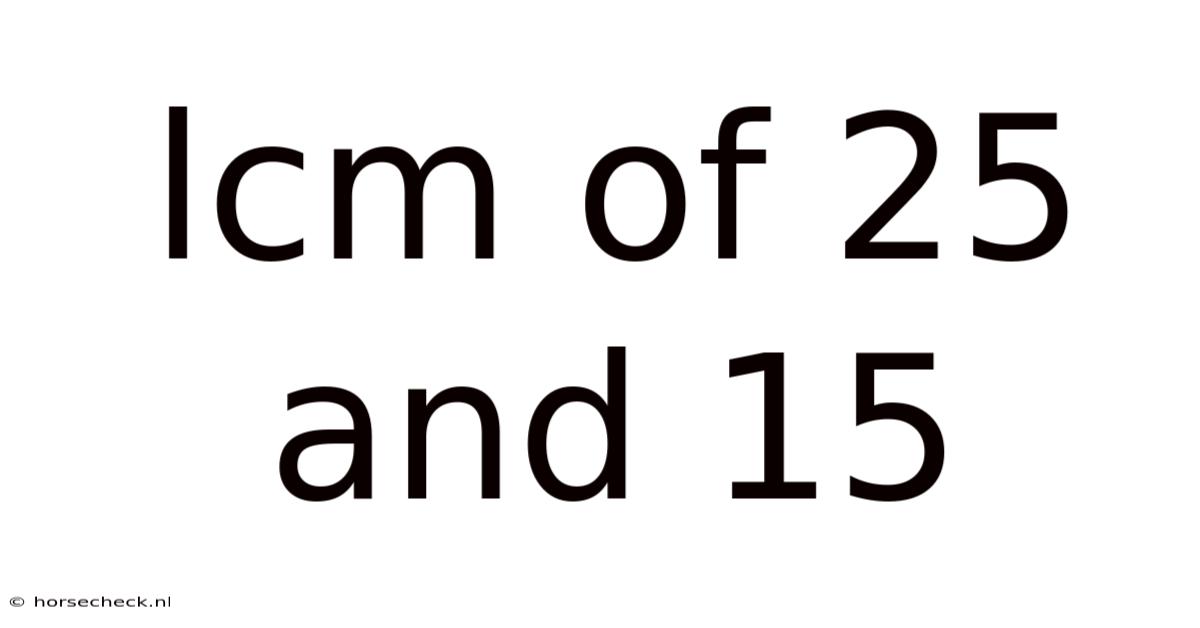
Table of Contents
Finding the LCM of 25 and 15: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it lays a strong foundation for more advanced mathematical concepts. This article will explore the LCM of 25 and 15 in detail, explaining multiple approaches, delving into the theoretical underpinnings, and answering frequently asked questions. We'll move beyond simply finding the answer and explore the why behind the calculations, making this a valuable resource for students and anyone looking to strengthen their understanding of number theory.
Introduction: What is a Least Common Multiple?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding LCMs is crucial in various mathematical applications, including simplifying fractions, solving problems involving cycles (like finding when events coincide), and working with rational expressions. For this article, we'll focus on finding the LCM of 25 and 15.
Method 1: Listing Multiples
One of the most straightforward methods for finding the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 25 and 15:
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165...
By comparing the lists, we can see that the smallest number appearing in both lists is 75. Therefore, the LCM of 25 and 15 is 75. While this method is simple for smaller numbers, it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and elegant method involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Let's find the prime factorization of 25 and 15:
- 25: 5 x 5 = 5²
- 15: 3 x 5
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together. In this case:
- The prime factors are 3 and 5.
- The highest power of 3 is 3¹ (from the factorization of 15).
- The highest power of 5 is 5² (from the factorization of 25).
Therefore, the LCM(25, 15) = 3¹ x 5² = 3 x 25 = 75. This method is generally faster and more efficient for larger numbers, as it avoids the lengthy process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a * b|) / GCD(a, b)
Let's find the GCD of 25 and 15 using the Euclidean algorithm:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the remainder (10) and repeat: 15 ÷ 10 = 1 with a remainder of 5.
- Repeat again: 10 ÷ 5 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 5.
Now, we can use the formula:
LCM(25, 15) = (25 * 15) / 5 = 375 / 5 = 75
This method demonstrates the elegant relationship between LCM and GCD, providing another efficient way to calculate the LCM.
Explanation with Venn Diagrams
Visualizing the LCM can be helpful, especially for beginners. We can represent the prime factorization of each number using a Venn diagram. For 25 and 15:
- 25: 5 x 5 (represented by two circles, each containing a '5')
- 15: 3 x 5 (represented by two circles, one containing a '3' and one containing a '5')
The overlapping area represents the common factors (in this case, a single '5'). The LCM is found by multiplying all the numbers in the diagram: 3 x 5 x 5 = 75. This visual approach provides an intuitive grasp of the concept.
Applications of LCM
Understanding LCMs is vital in various mathematical and real-world applications:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
- Scheduling and Cyclical Events: Imagine two machines that operate on different cycles. The LCM helps determine when both machines will be at their starting point simultaneously. For instance, if one machine completes a cycle every 25 minutes and another every 15 minutes, they'll both be at the start simultaneously after 75 minutes.
- Modular Arithmetic: LCMs play a crucial role in solving problems in modular arithmetic, a branch of number theory that deals with remainders.
- Music Theory: LCMs are used in music theory to determine the least common multiple of different note durations.
- Construction and Engineering: In applications involving repetitive patterns or cycles, LCM helps determine the synchronization and efficiency of processes.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors?
- A: If the numbers are relatively prime (meaning their GCD is 1), the LCM is simply their product. For example, LCM(15, 8) = 15 x 8 = 120.
-
Q: Can we find the LCM of more than two numbers?
- A: Yes, we can extend the prime factorization method or the GCD method to handle multiple numbers. For instance, to find the LCM of 15, 25, and 10, you would find the prime factorization of each number (15 = 3 x 5, 25 = 5 x 5, 10 = 2 x 5), and then take the highest power of each prime factor (2¹, 3¹, 5²) to get LCM(15, 25, 10) = 2 x 3 x 25 = 150.
-
Q: Why is the LCM important in everyday life?
- A: While you may not explicitly calculate LCMs daily, the underlying principles are used in many everyday situations involving scheduling, timing, and organization. Understanding LCMs enhances your problem-solving skills in various scenarios.
Conclusion: Mastering the LCM
Finding the least common multiple of 25 and 15, as demonstrated through various methods, is more than just an arithmetic exercise. It’s a stepping stone to understanding fundamental concepts in number theory, prime factorization, and the relationship between LCM and GCD. The ability to efficiently calculate LCMs is a valuable skill with applications extending far beyond the classroom, making it a worthwhile concept to master. Remember to practice using different methods to reinforce your understanding and choose the most efficient method depending on the numbers involved. Whether you prefer listing multiples, using prime factorization, or employing the GCD method, the crucial aspect is understanding the underlying principles and the significance of LCM in various mathematical and real-world contexts.
Latest Posts
Latest Posts
-
Whats 0 125 As A Fraction
Sep 25, 2025
-
What Is 18 Times 4
Sep 25, 2025
-
Convert 11 C To Fahrenheit
Sep 25, 2025
-
17 100 As A Percent
Sep 25, 2025
-
3 24 As A Percent
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 25 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.