Lcm Of 6 5 4
horsecheck
Sep 21, 2025 · 6 min read
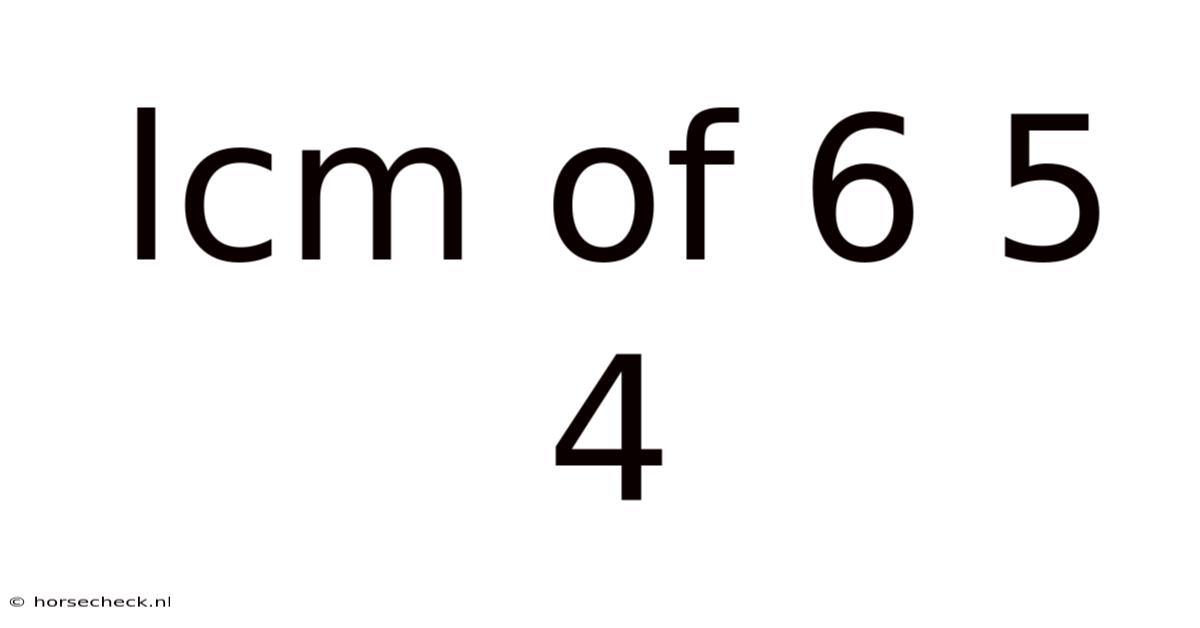
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 5, and 4: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction operations to complex scheduling problems. This article will provide a detailed explanation of how to calculate the LCM of 6, 5, and 4, exploring multiple methods and delving into the underlying mathematical principles. Understanding LCM is key for solving problems involving ratios, fractions, and cyclical events. We will break down the process step-by-step, ensuring even beginners can grasp the concept and confidently apply it.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's define what the least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
By examining the lists, we see that the smallest number present in all three lists is 60. Therefore, the LCM of 6, 5, and 4 is 60. This method is easy to visualize but becomes less efficient with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
-
Prime Factorization:
- 6 = 2 x 3
- 5 = 5
- 4 = 2 x 2 = 2²
-
Identify the highest power of each prime factor:
- The prime factors present are 2, 3, and 5.
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(6, 5, 4) = 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the LCM of 6, 5, and 4, using prime factorization, is 60. This method is more systematic and generally faster for larger numbers compared to listing multiples.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The LCM and the greatest common divisor (GCD) of two or more numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
While this formula is typically used for two numbers, it can be extended to multiple numbers by applying it iteratively. First, we find the GCD of two numbers, then use the result to find the GCD of the result with the third number, and so on. Let’s illustrate:
-
Find the GCD of 6 and 5: The GCD of 6 and 5 is 1 (as they share no common factors other than 1).
-
Find the LCM of 6 and 5: Using the formula LCM(a,b) * GCD(a,b) = a*b, we get LCM(6,5) * 1 = 6 * 5, therefore LCM(6,5) = 30.
-
Find the GCD of 30 and 4: The GCD of 30 and 4 is 2.
-
Find the LCM of 30 and 4: Using the formula again, LCM(30,4) * 2 = 30 * 4, therefore LCM(30,4) = 60.
Therefore, the LCM of 6, 5, and 4 using this method is 60. This method is efficient for larger numbers, especially when combined with algorithms for efficient GCD calculation like Euclid's algorithm.
Illustrative Examples: Real-World Applications of LCM
Understanding LCM is not just an abstract mathematical exercise; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine three buses arrive at a bus stop at intervals of 6, 5, and 4 minutes, respectively. To find when all three buses arrive simultaneously, we need to find the LCM of 6, 5, and 4, which is 60 minutes (or 1 hour).
-
Fraction Operations: When adding or subtracting fractions with different denominators, we need to find the LCM of the denominators to create a common denominator. This simplifies the calculation significantly. For example, adding 1/6 + 1/5 + 1/4 requires finding the LCM of 6, 5, and 4 (which is 60), allowing us to rewrite the fractions as 10/60 + 12/60 + 15/60 = 37/60.
-
Gear Ratios: In mechanics, gear ratios often involve finding common multiples to synchronize the movement of different gears.
-
Cyclical Events: Problems involving events that repeat at regular intervals (e.g., the phases of the moon, planetary orbits) often utilize the concept of LCM to determine when these events coincide.
Frequently Asked Questions (FAQ)
Q: What if the numbers have a common factor?
A: The prime factorization method handles common factors automatically. The highest power of each prime factor is considered, ensuring that the LCM is the smallest common multiple.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM. However, understanding the underlying methods is crucial for problem-solving and deeper mathematical understanding.
Q: What is the difference between LCM and GCD?
A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related but represent different aspects of the relationship between numbers.
Q: How do I find the LCM of more than three numbers?
A: You can extend the prime factorization method or the iterative GCD/LCM method to accommodate any number of integers. For example, to find the LCM of 6, 5, 4, and 3, you would first find the LCM of 6, 5, and 4 (which is 60), and then find the LCM of 60 and 3.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with far-reaching applications. While the listing multiples method is intuitive for smaller numbers, the prime factorization method offers a more efficient and elegant solution, particularly for larger numbers. Understanding the concept of LCM, coupled with the ability to employ different calculation methods, empowers you to solve a wide range of mathematical problems and understand the intricate relationships between numbers. Remember that mastering the LCM is not just about calculations; it’s about understanding the underlying principles and applying them to real-world problems. This understanding will serve you well in various aspects of mathematics and beyond.
Latest Posts
Latest Posts
-
Square Root Of 74 Simplified
Sep 22, 2025
-
Two Thirds Divided By Three
Sep 22, 2025
-
25 64 Vs 3 8
Sep 22, 2025
-
Divide 30 By 1 2
Sep 22, 2025
-
177 Degrees Celsius To Fahrenheit
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 5 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.