What Is 1/3 Of 10
horsecheck
Sep 23, 2025 · 5 min read
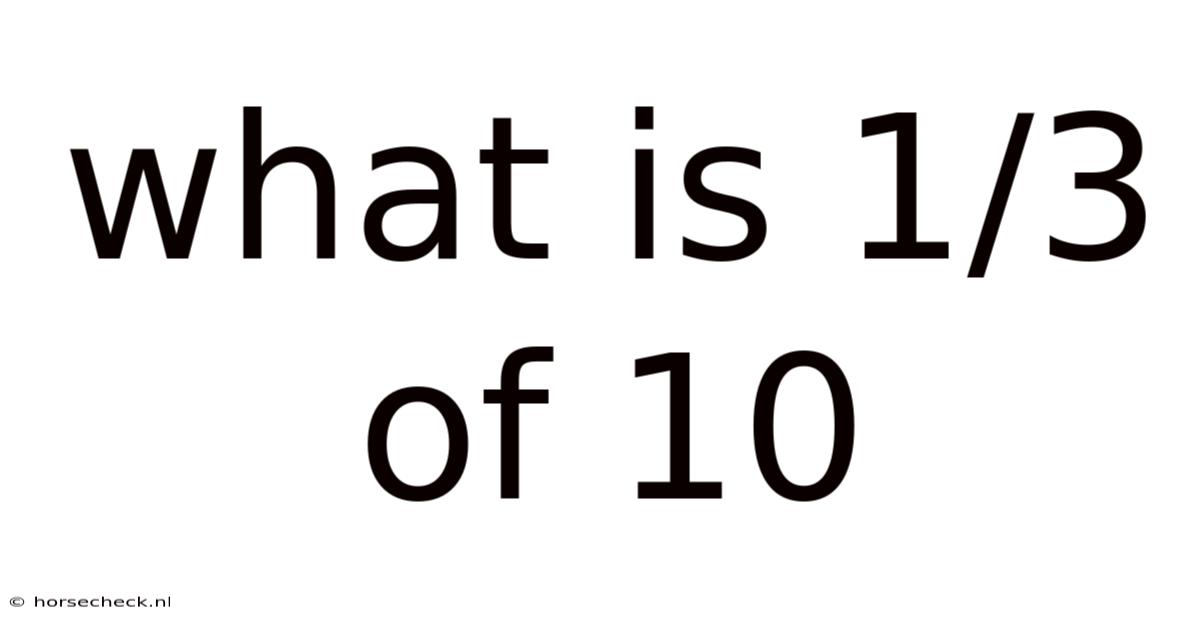
Table of Contents
What is 1/3 of 10? A Deep Dive into Fractions and Division
Finding 1/3 of 10 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic question opens doors to a deeper understanding of fractions, division, and their applications in various fields. This article will not only provide the answer but also explore the underlying concepts, different methods of solving the problem, and practical applications in everyday life. We'll even delve into some related mathematical concepts to solidify your understanding. By the end, you'll be equipped to tackle similar problems with confidence and a broader mathematical perspective.
Understanding Fractions: The Building Blocks
Before we tackle the problem of finding 1/3 of 10, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we are considering.
In the fraction 1/3, the numerator is 1 and the denominator is 3. This means we're considering one part out of a whole that's divided into three equal parts.
Method 1: Direct Multiplication
The most straightforward way to find 1/3 of 10 is to multiply 1/3 by 10:
(1/3) * 10 = 10/3
This result, 10/3, is an improper fraction because the numerator is larger than the denominator. To make it easier to understand, we convert it into a mixed number. We do this by dividing the numerator (10) by the denominator (3):
10 ÷ 3 = 3 with a remainder of 1
This means 10/3 can be expressed as 3 and 1/3, or 3 1/3. Therefore, 1/3 of 10 is 3 1/3.
Method 2: Division
Alternatively, we can approach this problem using division. Finding 1/3 of 10 is the same as dividing 10 into three equal parts.
10 ÷ 3 ≈ 3.333...
This gives us a decimal approximation of 3.333..., which is another way of representing 3 1/3. The three dots (...) indicate that the decimal continues infinitely, representing the recurring decimal 0.333...
Method 3: Visual Representation
Visualizing the problem can be particularly helpful for understanding fractions. Imagine a rectangle representing the number 10. To find 1/3 of 10, divide the rectangle into three equal parts. Each part represents 1/3 of 10. Since 10 divided by 3 is approximately 3.33, each part is approximately 3.33 units long.
Decimal Equivalents and Rounding
The decimal representation of 1/3 (0.333...) is a repeating decimal. This means the digit 3 repeats infinitely. In practical applications, you might need to round this decimal to a specific number of decimal places. For instance, rounding to two decimal places gives 3.33. However, it's important to remember that this is an approximation; the true value is 3 1/3.
Applications in Real-World Scenarios
Understanding how to find fractions of numbers has numerous real-world applications:
- Cooking: If a recipe calls for 1/3 cup of sugar for every 10 cookies, you'd need to calculate 1/3 of 10 to determine how much sugar to use for a batch of 10 cookies.
- Shopping: If an item is discounted by 1/3, and the original price is $10, you can calculate the discount amount by finding 1/3 of $10.
- Construction: In construction projects, accurate measurements are crucial. If a worker needs to cut a 10-meter beam into three equal parts, they need to understand how to find 1/3 of 10 meters.
- Data Analysis: Calculating proportions and percentages often involves working with fractions. Finding 1/3 of a dataset is a common task in statistical analysis.
Expanding the Concept: Fractions and Proportions
The problem of finding 1/3 of 10 is closely related to the concept of proportions. A proportion is a statement of equality between two ratios. For example:
1/3 = x/10
Here, we're saying that the ratio of 1 to 3 is equal to the ratio of x (the unknown quantity) to 10. To solve for x, we can cross-multiply:
3x = 10
x = 10/3 = 3 1/3
Further Exploration: Working with More Complex Fractions
Once you master finding 1/3 of 10, you can extend your knowledge to more complex fraction problems. For example, you could try finding 2/5 of 15, or 3/7 of 21. These problems require the same fundamental principles: multiplication or division, and the conversion between improper fractions and mixed numbers.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to find 1/3 of 10?
A: Yes, you can. Simply enter (1/3) * 10 or 10 ÷ 3 into your calculator. The result will be a decimal approximation, such as 3.333... Remember that this is an approximation of the exact value, which is 3 1/3.
Q: Why is 1/3 expressed as a repeating decimal?
A: The fraction 1/3 represents a rational number, but its decimal representation is non-terminating and repeating because the denominator (3) contains a prime factor (3) other than 2 or 5, which are the prime factors of 10 (the base of our decimal system).
Q: What if the problem involved finding a different fraction of 10, say 2/3 of 10?
A: You would follow the same principles. To find 2/3 of 10, you would multiply (2/3) * 10 = 20/3 = 6 2/3.
Conclusion: Mastering Fractions for a Brighter Future
Finding 1/3 of 10, while seemingly simple, provides a valuable foundation for understanding fractions, division, and their applications in various contexts. By mastering these fundamental concepts, you'll be better equipped to tackle more complex mathematical problems and apply these skills to real-world situations. Remember to practice regularly and explore different methods of solving fraction problems to solidify your understanding. From cooking to construction, from shopping to data analysis, understanding fractions is a crucial skill that transcends the classroom and empowers you in everyday life. The more you practice, the more confident you will become in handling fractions and related mathematical concepts. So keep practicing, keep exploring, and keep learning!
Latest Posts
Latest Posts
-
Lcm Of 18 And 15
Sep 23, 2025
-
What Are Factors Of 87
Sep 23, 2025
-
Whats 19 32 In Inches
Sep 23, 2025
-
What Grade Is A 8 12
Sep 23, 2025
-
What Is 15 Of 11
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.