What Is 1/6 Of 18
horsecheck
Sep 24, 2025 · 6 min read
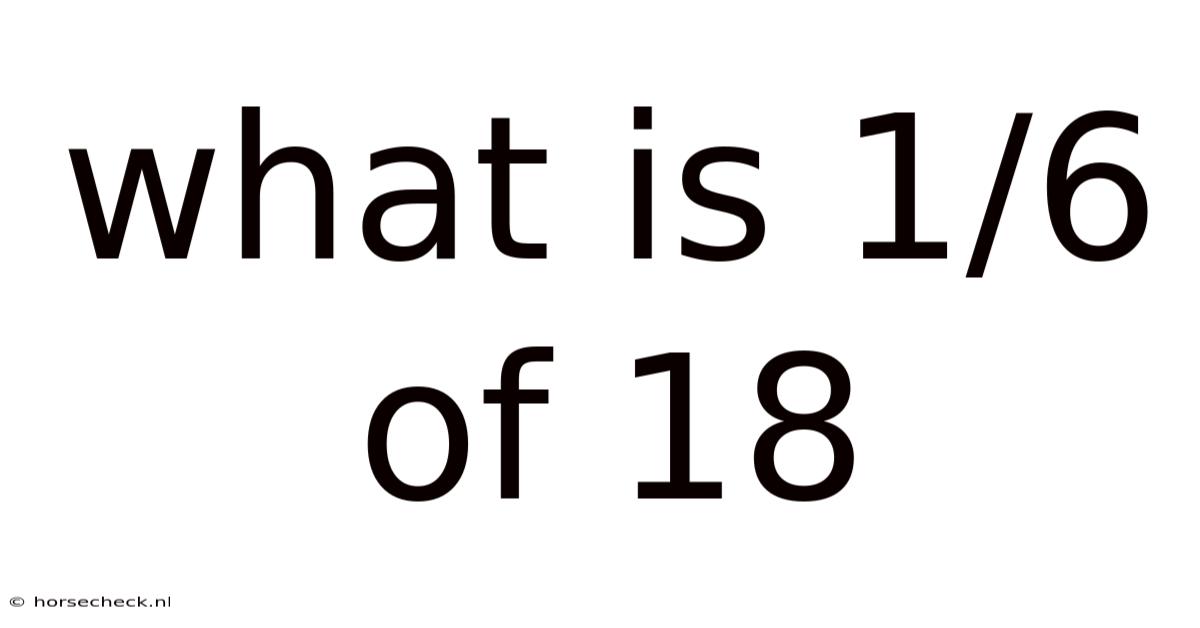
Table of Contents
What is 1/6 of 18? A Deep Dive into Fractions and Their Applications
Finding 1/6 of 18 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic equation opens the door to a much broader comprehension of fractions, their practical applications, and their role in more complex mathematical concepts. This article will not only answer the question "What is 1/6 of 18?" but will also explore the underlying principles, provide various methods for solving similar problems, and discuss real-world examples where this type of calculation is crucial.
Introduction: Understanding Fractions
Before we delve into the specifics of finding 1/6 of 18, let's establish a firm understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/6, the denominator (6) signifies that the whole is divided into six equal parts. The numerator (1) represents one of those six parts. Therefore, 1/6 represents one-sixth of the whole.
Methods for Calculating 1/6 of 18
There are several ways to calculate 1/6 of 18. Let's explore the most common and intuitive approaches:
1. Multiplication:
The most straightforward method is to multiply the fraction (1/6) by the whole number (18). This can be expressed as:
(1/6) * 18 = 18/6
This results in an improper fraction (where the numerator is larger than the denominator). To simplify this, we divide the numerator (18) by the denominator (6):
18 ÷ 6 = 3
Therefore, 1/6 of 18 is 3.
2. Division:
Alternatively, we can solve this problem using division. Since we're looking for one-sixth of 18, we can divide 18 by 6:
18 ÷ 6 = 3
This directly gives us the answer: 3. This method highlights the inherent relationship between fractions and division. The fraction 1/6 essentially signifies the operation of dividing by 6.
3. Visual Representation:
A visual approach can be particularly helpful for understanding the concept, especially for beginners. Imagine a pizza cut into 6 equal slices. 1/6 of the pizza represents one slice. If you have 18 slices (representing the number 18), finding 1/6 of 18 means determining how many slices constitute one-sixth of the total. This visual representation clearly illustrates that 1/6 of 18 is 3 slices.
Expanding the Concept: Working with Different Fractions and Whole Numbers
The methods described above are applicable to calculating a fraction of any whole number. Let's consider a few examples to reinforce our understanding:
-
Finding 2/3 of 15: This can be calculated as (2/3) * 15 = 30/3 = 10. Alternatively, we can find 1/3 of 15 (which is 5) and then multiply by 2 to get 10.
-
Finding 3/4 of 20: This can be calculated as (3/4) * 20 = 60/4 = 15. Or, we can find 1/4 of 20 (which is 5) and then multiply by 3 to get 15.
-
Finding 5/8 of 32: This can be calculated as (5/8) * 32 = 160/8 = 20. Or, we can find 1/8 of 32 (which is 4) and then multiply by 5 to get 20.
These examples showcase the versatility and applicability of the multiplication and division methods in solving fraction-related problems.
Real-World Applications: Where Fractions Matter
Understanding fractions is not just a classroom exercise; it's a fundamental skill with numerous real-world applications:
-
Cooking and Baking: Recipes often require fractions of ingredients (e.g., 1/2 cup of sugar, 2/3 cup of flour). Accurate calculations ensure the dish turns out as expected.
-
Measurement and Construction: Construction workers, engineers, and architects use fractions extensively in their measurements and calculations to ensure precision and accuracy in building structures.
-
Finance and Budgeting: Fractions are crucial in understanding percentages, interest rates, and calculating portions of budgets. For instance, determining a 1/6 share of profits in a business partnership involves this type of calculation.
-
Data Analysis and Statistics: Fractions play a vital role in representing and interpreting data, calculating proportions, and making inferences.
-
Sharing and Division: Everyday situations like sharing a pizza, dividing tasks amongst a group, or allocating resources involve using fractions to ensure fair distribution.
Frequently Asked Questions (FAQs)
Q: What if the fraction and the whole number don't divide evenly?
A: If the numerator and denominator don't divide evenly, you'll end up with a fraction as the answer. For example, 1/3 of 10 is (1/3)*10 = 10/3, which is an improper fraction (approximately 3.33). You can express this as a mixed number (3 1/3) or a decimal (3.33).
Q: How can I simplify a fraction?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD. For example, to simplify 12/18, the GCD is 6. Dividing both the numerator and denominator by 6 gives us 2/3, which is the simplified form.
Q: Are there online tools or calculators that can help with fraction calculations?
A: Yes, many online calculators and tools are available to perform fraction calculations, including addition, subtraction, multiplication, and division. These tools can be very helpful, particularly when working with more complex fractions.
Q: Why is understanding fractions important?
A: Understanding fractions is essential for developing strong mathematical foundations. It's a building block for more advanced concepts in algebra, geometry, calculus, and numerous other fields. Proficiency with fractions improves problem-solving skills and analytical thinking in various contexts.
Conclusion: Beyond the Basics of 1/6 of 18
While seemingly simple, the question "What is 1/6 of 18?" opens up a comprehensive exploration of fractions and their profound significance in mathematics and everyday life. Understanding the different methods for calculating fractions, including multiplication, division, and visual representations, strengthens numerical literacy and enhances problem-solving abilities. The ability to work comfortably with fractions is a crucial skill that extends far beyond the classroom and into many facets of daily life, impacting various fields from culinary arts to engineering and finance. Mastering fractions is not just about finding the answer; it’s about developing a deeper understanding of the underlying mathematical concepts and their widespread applications. Therefore, let's embrace the power of fractions and equip ourselves with the knowledge and confidence to confidently tackle any fraction-related challenges we may encounter.
Latest Posts
Latest Posts
-
Hcf Of 3 And 5
Sep 24, 2025
-
What Is 50 Of 8
Sep 24, 2025
-
What Is 20 Of 36 00
Sep 24, 2025
-
Is 207 A Prime Number
Sep 24, 2025
-
What Is A 12 20
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/6 Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.