What Is 10 Of 39
horsecheck
Sep 22, 2025 · 6 min read
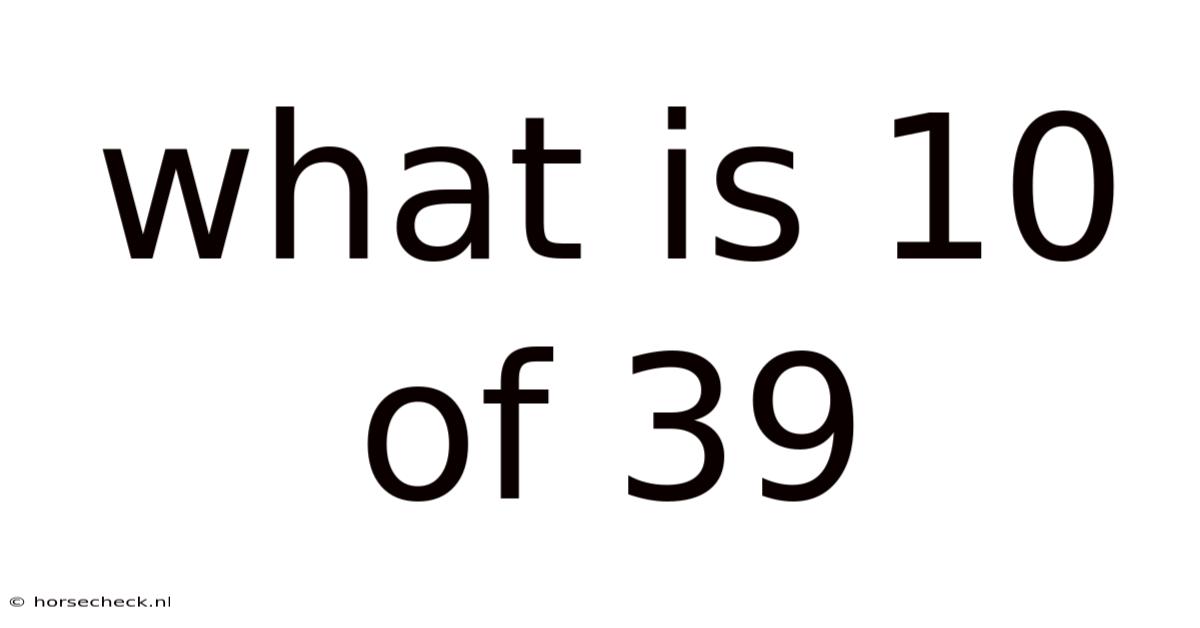
Table of Contents
What is 10 of 39? Understanding Fractions, Percentages, and Ratios
This article explores the multifaceted meaning of "10 of 39," delving beyond the simple statement to uncover its significance in various mathematical contexts. We'll examine how to represent this relationship as a fraction, a percentage, and a ratio, and explore practical applications where understanding this concept becomes crucial. This explanation will be thorough, providing a deep understanding suitable for learners of all levels.
Understanding the Basic Relationship
At its core, "10 of 39" describes a part-to-whole relationship. We have a smaller quantity (10) that represents a portion of a larger quantity (39). This fundamental concept underpins numerous mathematical operations and real-world scenarios. Let's examine how to express this relationship using different mathematical tools.
Representing "10 of 39" as a Fraction
A fraction is a numerical representation of a part of a whole. In this case, 10 represents the part, and 39 represents the whole. Therefore, "10 of 39" can be expressed as the fraction 10/39. This fraction is in its simplest form because 10 and 39 share no common factors other than 1.
This fraction directly indicates the proportion of 10 relative to 39. It helps visualize the relative size of the part compared to the whole. For instance, if you have a bag containing 39 marbles, and 10 of them are red, the fraction 10/39 represents the proportion of red marbles in the bag.
Understanding Fraction Simplification: It's important to note that fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 10 and 39 is 1, meaning the fraction is already in its simplest form. If, for example, we had "10 of 50", this would be represented as 10/50, which simplifies to 1/5 after dividing both numerator and denominator by their GCD of 10.
Converting "10 of 39" to a Percentage
A percentage expresses a fraction as a proportion of 100. To convert the fraction 10/39 to a percentage, we perform the following calculation:
(10/39) * 100%
This calculation yields approximately 25.64%. This means that 10 represents approximately 25.64% of 39. The percentage provides a readily understandable way to express the proportional relationship, especially when comparing different proportions. For example, comparing 10 out of 39 to 15 out of 50 becomes easier when we use percentages (25.64% vs 30%).
Precision in Calculations: When working with percentages, it's crucial to maintain accuracy. Rounding to a specific number of decimal places depends on the required level of precision for the particular application. In some cases, using the exact fraction 10/39 might be preferred for greater accuracy.
Expressing "10 of 39" as a Ratio
A ratio expresses the relative sizes of two or more quantities. In the case of "10 of 39," the ratio is expressed as 10:39. This ratio reads as "10 to 39" and indicates that for every 10 units of one quantity, there are 39 units of the total quantity. Ratios are often used to compare quantities or to describe proportions.
Ratios can also be expressed in simplified form if both numbers share a common factor. Since 10 and 39 share only the factor 1, the ratio 10:39 is already in its simplest form. However, if we consider "10 out of 20", the ratio would be 10:20, which simplifies to 1:2.
Real-World Applications of "10 of 39"
Understanding the representation of "10 of 39" as a fraction, percentage, or ratio is crucial in various real-world scenarios. Consider these examples:
-
Statistics and Probability: If 10 out of 39 participants in a survey answered "yes" to a particular question, the fraction 10/39, percentage 25.64%, or ratio 10:39 would represent the proportion of "yes" responses. This data is essential for analyzing survey results and drawing conclusions.
-
Business and Finance: In business, understanding proportions is crucial. For example, if a company has 39 employees, and 10 of them are in the sales department, the ratio 10:39 or the percentage 25.64% can highlight the size and proportion of the sales team within the company.
-
Science and Engineering: In experimental science, proportions are frequently used. If 10 out of 39 trials produce a particular result, the fraction 10/39 can help determine the probability of that result.
-
Everyday Life: Imagine you are baking a cake that requires 39 ingredients, and you have already added 10 of them. The fraction 10/39 or the percentage 25.64% shows the progress of your baking.
Further Exploration: Working with Proportions
Understanding "10 of 39" extends beyond simple representation. Let's explore how to use proportions to solve problems involving similar relationships.
For instance, if you know that 10 out of 39 apples are bad, and you have a total of 117 apples, how many bad apples would you expect to find? This is solved using proportions:
10/39 = x/117
To solve for x (the number of bad apples in 117), we cross-multiply:
39x = 10 * 117
39x = 1170
x = 1170 / 39
x = 30
Therefore, you would expect to find 30 bad apples in a batch of 117 apples. This demonstrates how understanding the relationship between 10 and 39, and representing it as a fraction, allows us to solve for unknowns in proportional situations.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 10/39?
A: 10/39 is already in its simplest form because 10 and 39 have no common factors other than 1.
Q: How do I convert a fraction to a percentage?
A: Multiply the fraction by 100%. For example, to convert 10/39 to a percentage, calculate (10/39) * 100%.
Q: What is the difference between a ratio and a fraction?
A: Both ratios and fractions express a relationship between quantities. However, fractions represent a part-to-whole relationship, while ratios compare two or more quantities.
Q: Are there any online tools to help with fraction, percentage, and ratio calculations?
A: While I cannot provide external links, a simple online search for "fraction calculator," "percentage calculator," or "ratio calculator" will reveal numerous resources available.
Q: How accurate should my percentage calculations be?
A: The level of accuracy required depends on the context. For some applications, rounding to one or two decimal places might be sufficient. In other cases, greater accuracy may be necessary. Using the original fraction avoids rounding errors.
Conclusion: The Significance of Understanding Proportions
Understanding "10 of 39" goes beyond a simple arithmetic statement. It provides a foundation for grasping the concepts of fractions, percentages, and ratios—critical tools in mathematics and various fields. By mastering these concepts, you enhance your ability to analyze data, solve problems, and interpret information in a more comprehensive and meaningful way. This knowledge is transferable to various aspects of life, from everyday tasks to complex scientific investigations. Remember the importance of accuracy and choosing the most appropriate representation (fraction, percentage, or ratio) based on the context of the problem.
Latest Posts
Latest Posts
-
Gcf Of 16 And 30
Sep 22, 2025
-
Square Root Of 1 49
Sep 22, 2025
-
40c Is What In F
Sep 22, 2025
-
What Is 1 3 9
Sep 22, 2025
-
What Is 1 4 Of 40
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.