What Is 2/3 Of 60
horsecheck
Sep 23, 2025 · 6 min read
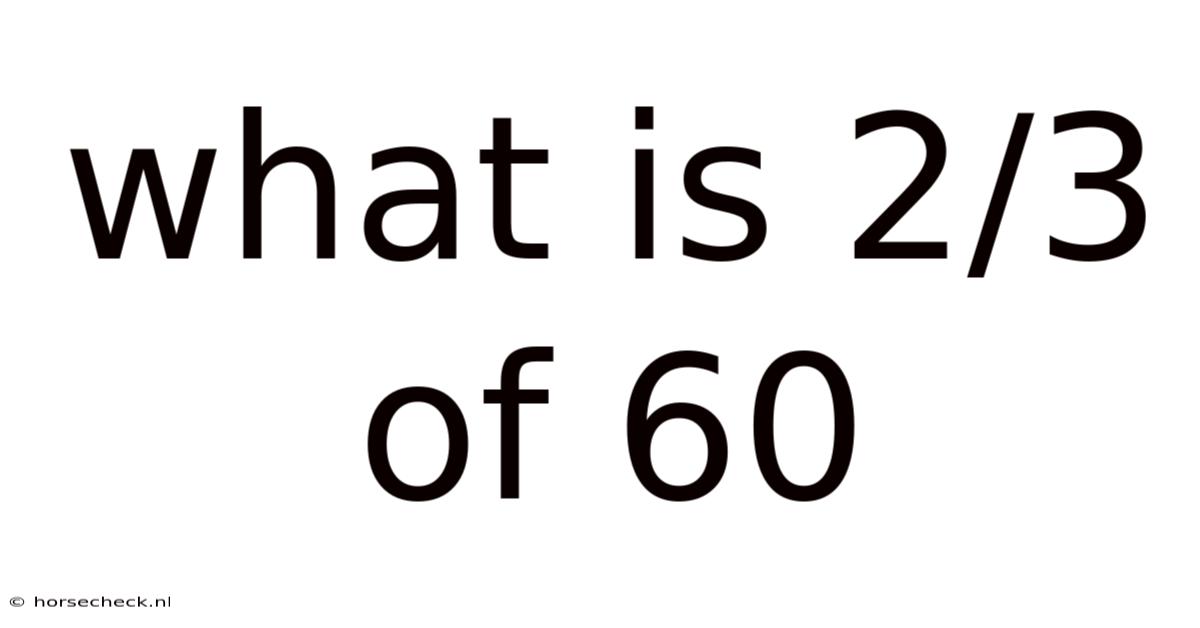
Table of Contents
What is 2/3 of 60? A Deep Dive into Fractions and their Applications
Finding 2/3 of 60 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to solve this seemingly straightforward question unlocks a deeper understanding of fractions, their practical applications, and even more advanced mathematical concepts. This article will not only show you how to calculate 2/3 of 60 but will also explore the underlying principles, provide various methods for solving similar problems, and delve into real-world examples where this type of calculation is crucial. By the end, you’ll be confident in tackling fraction problems and appreciating their significance beyond the classroom.
Understanding Fractions: The Building Blocks
Before we dive into calculating 2/3 of 60, let's establish a solid foundation in understanding fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number (in this case, 2) indicates how many parts we're considering.
- Denominator: The bottom number (in this case, 3) indicates the total number of equal parts the whole is divided into.
Therefore, 2/3 means we're dealing with 2 out of 3 equal parts of a whole.
Method 1: Multiplication – The Direct Approach
The most straightforward way to find 2/3 of 60 is through multiplication. We can express "of" as multiplication. So, "2/3 of 60" translates to:
(2/3) * 60
To perform this calculation:
- Multiply the numerator by the whole number: 2 * 60 = 120
- Divide the result by the denominator: 120 / 3 = 40
Therefore, 2/3 of 60 is 40.
Method 2: Finding One-Third and Doubling – A Step-by-Step Approach
This method is particularly helpful for visualizing the problem and is excellent for beginners.
- Find one-third: Divide 60 by the denominator (3): 60 / 3 = 20. This means one-third of 60 is 20.
- Double the result: Since we need two-thirds, we multiply the value of one-third by 2: 20 * 2 = 40.
Again, we arrive at the answer: 2/3 of 60 is 40.
Method 3: Converting the Fraction to a Decimal – Using Decimal Equivalents
Fractions can be converted into decimals for easier calculation, especially when using a calculator.
- Convert the fraction to a decimal: Divide the numerator by the denominator: 2 / 3 ≈ 0.6667 (we'll use a rounded value for simplicity)
- Multiply the decimal by the whole number: 0.6667 * 60 ≈ 40
While the decimal approach might introduce minor rounding errors depending on the level of precision, it offers a convenient alternative, particularly for larger or more complex fractions. Note that using the exact fractional representation avoids any rounding error.
Real-World Applications: Where Fractions Matter
Understanding fractions and how to calculate them is not just about passing math tests. It's a fundamental skill with numerous real-world applications across various fields:
- Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of flour, 2/3 cup of sugar). Accurate calculations are essential for successful outcomes.
- Construction and Engineering: Precision in measurements is critical. Fractions are used extensively in blueprints, calculations, and material estimations.
- Finance and Budgeting: Managing finances often involves working with percentages (which are essentially fractions expressed as parts of 100), calculating interest, and understanding proportions.
- Data Analysis and Statistics: Understanding proportions and representing data often requires working with fractions and percentages.
- Everyday Life: Sharing items fairly, calculating discounts, understanding sales, and even comparing prices often involve fractional calculations.
Expanding the Concept: Working with Different Fractions and Whole Numbers
The principles discussed above can be applied to any fraction and whole number. Let's consider a few examples:
- Finding 3/4 of 80: (3/4) * 80 = (3 * 80) / 4 = 240 / 4 = 60
- Finding 5/6 of 36: (5/6) * 36 = (5 * 36) / 6 = 180 / 6 = 30
- Finding 1/5 of 100: (1/5) * 100 = (1 * 100) / 5 = 100 / 5 = 20
These examples demonstrate the versatility and consistent application of the multiplication and division methods.
Beyond the Basics: Introducing More Complex Scenarios
While the problem "What is 2/3 of 60?" is relatively simple, it serves as a stepping stone to more complex fractional calculations. Consider these extensions:
- Fractions with larger numbers: Calculating 27/32 of 512 requires the same principles but involves larger numbers.
- Mixed numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/2). Calculating a fraction of a mixed number requires converting it to an improper fraction first. For example, to find 1/3 of 2 1/2, we first convert 2 1/2 to 5/2, then calculate (1/3) * (5/2) = 5/6.
- Multiple fractions: Calculations might involve finding a fraction of a fraction, which requires multiplying the fractions together. For instance, to find 1/2 of 2/3, we multiply (1/2) * (2/3) = 2/6 = 1/3.
Mastering the fundamentals laid out earlier provides a firm base for tackling these more advanced scenarios.
Troubleshooting Common Mistakes
While seemingly straightforward, several common errors can occur when working with fractions:
- Incorrect order of operations: Always perform multiplication before division when dealing with fractions and whole numbers.
- Mistakes in division: Double-check your division calculations to ensure accuracy.
- Incorrect simplification: Always simplify the fraction to its lowest terms after calculation. For example, 2/6 should be simplified to 1/3.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to calculate fractions?
A1: Fractions are essential for understanding proportions, ratios, and percentages. These concepts are ubiquitous in many aspects of life, from finance and cooking to science and engineering.
Q2: What if the whole number isn't evenly divisible by the denominator?
A2: You will still perform the multiplication and division as usual. You may get a fraction or a decimal as a result.
Q3: Are there any online resources or tools to help with fraction calculations?
A3: While I cannot provide external links, many online calculators and educational websites offer tools to assist with fraction calculations.
Q4: How can I improve my skills in working with fractions?
A4: Consistent practice is key. Start with simpler problems and gradually work your way up to more complex ones. Use visual aids like diagrams to better understand the concepts. Look for additional practice exercises in textbooks or online resources.
Conclusion: Mastering Fractions – A Journey, Not a Destination
Calculating 2/3 of 60, while seemingly elementary, serves as a crucial gateway to understanding fractions and their pervasive applications. By mastering these fundamental principles, you equip yourself with a powerful tool applicable across various fields. Remember that consistent practice, a clear understanding of the concepts, and attention to detail are key to success in tackling any fractional problem, no matter how complex it may appear. The journey of mastering fractions is an ongoing process of learning, exploration, and problem-solving – a journey well worth undertaking.
Latest Posts
Latest Posts
-
Gcf Of 70 And 28
Sep 23, 2025
-
64 To The 2 3 Power
Sep 23, 2025
-
What Is 5 Of 18
Sep 23, 2025
-
Convert 85 F To Celsius
Sep 23, 2025
-
14 35 In Simplest Form
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.