What Is 2.56 Of 25
horsecheck
Sep 25, 2025 · 5 min read
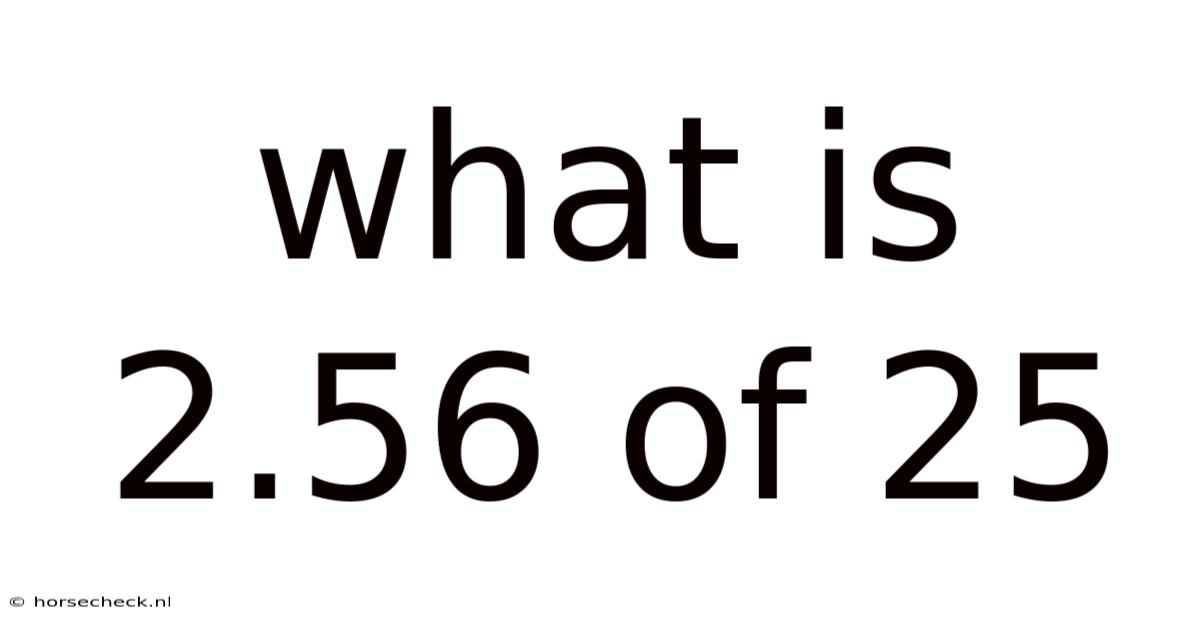
Table of Contents
What is 2.56% of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will delve into the seemingly simple question, "What is 2.56% of 25?", but will expand upon this to provide a complete understanding of percentage calculations, including different methods, real-world examples, and troubleshooting common errors. This guide will equip you with the knowledge to confidently tackle any percentage problem you encounter.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent percentage. Essentially, a percentage shows a proportional relationship between a part and a whole. For example, 50% means 50 out of 100, or one-half.
The key to understanding percentage calculations is recognizing the relationship between the percentage, the part, and the whole. We can represent this relationship with a simple formula:
(Percentage/100) x Whole = Part
Or, rearranged to find the percentage:
(Part/Whole) x 100 = Percentage
Calculating 2.56% of 25: Method 1 - The Formula Approach
Let's apply the formula to solve "What is 2.56% of 25?".
In this case:
- Percentage: 2.56
- Whole: 25
- Part: This is what we need to calculate.
Using the formula:
(2.56/100) x 25 = Part
0.0256 x 25 = 0.64
Therefore, 2.56% of 25 is 0.64.
Calculating 2.56% of 25: Method 2 - Decimal Conversion
Another way to solve this is by converting the percentage to a decimal. To convert a percentage to a decimal, simply divide the percentage by 100.
2.56% ÷ 100 = 0.0256
Now, multiply this decimal by the whole number:
0.0256 x 25 = 0.64
Again, we arrive at the answer: 2.56% of 25 is 0.64.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life. Here are some examples:
-
Shopping Discounts: If a store offers a 20% discount on a $50 item, you can easily calculate the discount amount and the final price using percentage calculations.
-
Sales Tax: Calculating the sales tax on a purchase requires understanding percentages. If the sales tax rate is 6%, you'll need to calculate 6% of the purchase price to determine the total cost.
-
Interest Rates: Understanding interest rates on loans, savings accounts, and investments heavily relies on percentage calculations. You need to understand how interest is calculated to make informed financial decisions.
-
Tip Calculations: When dining out, calculating a tip (e.g., 15% or 20% of the bill) requires knowledge of percentage calculations.
-
Grade Calculation: Many academic grading systems use percentages to represent a student's performance. Understanding percentages helps students track their progress and teachers assess student learning.
-
Statistical Analysis: Percentages are frequently used in statistical data to represent proportions and trends. This is important for interpreting data accurately.
Beyond the Basics: Advanced Percentage Problems
While calculating 2.56% of 25 is a straightforward example, percentage problems can become more complex. Let's explore some variations:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage using the formula: (Part/Whole) x 100 = Percentage. For example, if 5 out of 20 students passed an exam, the percentage of students who passed is (5/20) x 100 = 25%.
-
Finding the Whole: If you know the part and the percentage, you can calculate the whole using the formula: (Part / (Percentage/100)) = Whole. For instance, if 10 is 20% of a number, the number is (10 / (20/100)) = 50.
-
Percentage Increase/Decrease: Calculating percentage change involves finding the difference between two values and expressing it as a percentage of the original value. The formula is: [(New Value - Original Value) / Original Value] x 100. A positive result indicates an increase, while a negative result indicates a decrease.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires a more complex formula involving exponents.
Troubleshooting Common Percentage Errors
Several common mistakes can occur when working with percentages. Let's address some of them:
-
Incorrect Decimal Conversion: A frequent error is incorrectly converting a percentage to a decimal. Remember to divide the percentage by 100. For example, 5% is 0.05, not 0.5.
-
Mixing Up Part and Whole: Ensure you correctly identify the part and the whole in the problem. The whole represents the total amount, while the part represents a portion of the whole.
-
Incorrect Formula Application: Carefully apply the correct formula based on what you are trying to calculate (percentage, part, or whole).
-
Calculation Mistakes: Double-check your calculations to avoid simple arithmetic errors. Using a calculator can help minimize these errors.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Yes, using a calculator is highly recommended, especially for more complex percentage calculations. Most calculators have a percentage function (%) that simplifies the process.
Q: What if the percentage is a fraction or decimal itself?
A: The same principles apply. Convert the percentage to a decimal and then multiply by the whole number. For example, to find 0.25% of 100, convert 0.25% to 0.0025 and multiply by 100 to get 0.25.
Q: How do I calculate percentage increase or decrease?
A: Use the formula: [(New Value - Original Value) / Original Value] x 100. A positive result signifies an increase, and a negative result signifies a decrease.
Q: Are there online percentage calculators available?
A: Yes, numerous online calculators can help you perform various percentage calculations quickly and easily. However, understanding the underlying principles is essential for problem-solving and critical thinking.
Conclusion
Calculating percentages is a vital mathematical skill with broad applications in various aspects of life. While the seemingly simple question "What is 2.56% of 25?" serves as a starting point, it opens the door to understanding complex percentage calculations and their relevance in everyday situations. By mastering the formulas, methods, and troubleshooting techniques outlined in this comprehensive guide, you'll be well-equipped to confidently tackle any percentage problem, enhancing your mathematical abilities and empowering your decision-making skills in numerous contexts. Remember to practice regularly to solidify your understanding and build your confidence in this essential mathematical skill.
Latest Posts
Latest Posts
-
Gcf For 30 And 18
Sep 25, 2025
-
What Is 80 Of 23
Sep 25, 2025
-
All Factor Pairs Of 24
Sep 25, 2025
-
What Is 1600 Square Root
Sep 25, 2025
-
45 45 45
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.56 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.