What Is 25 X 10
horsecheck
Sep 22, 2025 · 6 min read
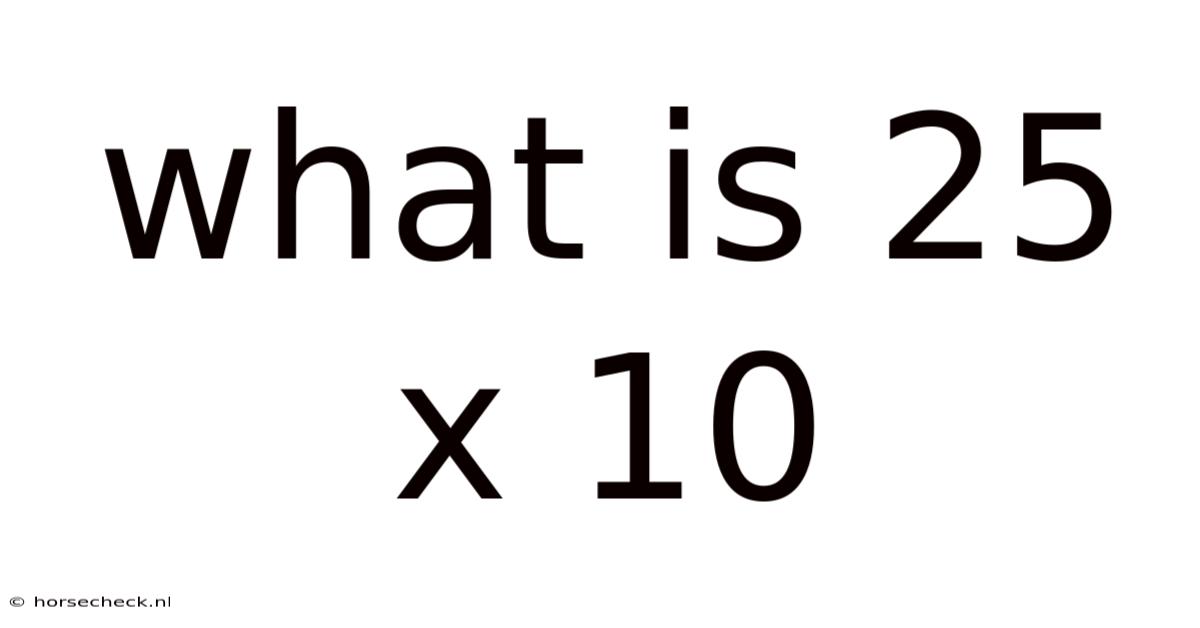
Table of Contents
What is 25 x 10? A Deep Dive into Multiplication and its Applications
This seemingly simple question, "What is 25 x 10?", opens a door to a vast world of mathematical concepts, practical applications, and problem-solving strategies. While the answer itself is straightforward – 250 – understanding the underlying principles behind this calculation provides a foundation for more complex mathematical endeavors. This article explores the multiplication operation, delves into various methods for solving this specific problem, and expands upon its significance in everyday life and various fields of study.
Understanding Multiplication: Beyond Rote Memorization
Multiplication is a fundamental arithmetic operation representing repeated addition. In essence, 25 x 10 means adding 25 to itself ten times: 25 + 25 + 25 + 25 + 25 + 25 + 25 + 25 + 25 + 25 = 250. While this approach works, it becomes inefficient for larger numbers. Multiplication provides a shortcut, a more efficient way to perform repeated addition.
Understanding multiplication involves grasping the concepts of:
- Multiplicand: The number being multiplied (in this case, 25).
- Multiplier: The number indicating how many times the multiplicand is added (in this case, 10).
- Product: The result of the multiplication (250).
These terms help establish a consistent vocabulary for discussing multiplication problems, irrespective of their complexity.
Methods for Calculating 25 x 10
Several methods can be used to calculate 25 x 10, each offering a unique perspective and level of understanding:
1. Repeated Addition: As mentioned earlier, this method involves adding 25 ten times. While straightforward, it's impractical for larger numbers.
2. Multiplication by 10 as a Shortcut: Multiplying by 10 is a particularly simple operation. Notice a pattern: when you multiply any whole number by 10, you simply add a zero to the end of the number. Thus, 25 x 10 = 250. This method relies on understanding place value in the decimal system. Each digit represents a power of 10 (ones, tens, hundreds, etc.), and multiplying by 10 shifts each digit one place to the left, effectively adding a zero.
3. Distributive Property: The distributive property of multiplication over addition allows us to break down complex problems into smaller, more manageable ones. While less efficient for this specific problem, it illustrates a crucial mathematical principle. We can rewrite 25 as (20 + 5). Then, applying the distributive property:
(20 + 5) x 10 = (20 x 10) + (5 x 10) = 200 + 50 = 250
4. Using a Multiplication Table: Multiplication tables provide a quick reference for common multiplication facts. A well-memorized multiplication table allows for instant recall of the product of 25 and 10.
5. Visual Representation: Visual aids, such as arrays or diagrams, can help visualize the multiplication process. An array of 25 rows and 10 columns would contain 250 individual units, representing the product.
The Significance of 25 x 10: Real-World Applications
The seemingly simple calculation of 25 x 10 appears frequently in everyday life and across various disciplines:
- Finance: Calculating the total cost of 25 items priced at $10 each.
- Measurement: Converting 25 centimeters to millimeters (1 cm = 10 mm).
- Geometry: Determining the area of a rectangle with a length of 25 units and a width of 10 units.
- Data Analysis: In statistics, multiplying frequencies or probabilities by 10 can be a common step in calculations.
- Programming: This basic multiplication forms the basis for more complex calculations within computer programs.
- Engineering: Many engineering calculations involve multiplication as a fundamental step, even if it's part of a larger, more complex equation.
Expanding the Concept: Multiplying Larger Numbers
The principles underlying 25 x 10 apply to much larger numbers. Consider the following examples:
- 25 x 100: Adding two zeros to the end of 25 gives us 2500. This extends the place value concept.
- 25 x 1000: Adding three zeros to the end of 25 gives us 25000.
- 25 x 10,000: Adding four zeros to the end of 25 gives us 250,000.
This demonstrates the efficiency and power of understanding the patterns inherent in multiplication. The multiplication by powers of 10 (10, 100, 1000, etc.) always results in adding the same number of zeros to the end of the multiplicand.
Exploring Related Concepts: Division, Fractions, and Decimals
The inverse operation of multiplication is division. Just as 25 x 10 = 250, 250 ÷ 10 = 25 and 250 ÷ 25 = 10. Understanding this relationship provides a deeper understanding of the interconnectedness of arithmetic operations.
Furthermore, fractions and decimals are closely related to multiplication. For instance, 25 x 10 can be expressed as a fraction (25/1 x 10/1 = 250/1 = 250) or as a decimal calculation (25.0 x 10.0 = 250.0). Understanding these connections provides a holistic understanding of numerical representation.
Addressing Potential Challenges and Misconceptions
While multiplication is a fundamental concept, some learners may encounter challenges:
- Place Value Confusion: Incorrect placement of digits during multiplication, especially when dealing with larger numbers.
- Memorization Difficulties: Difficulty remembering multiplication facts from the times table.
- Understanding the Concept: Difficulty grasping the underlying principle of repeated addition.
Overcoming these challenges requires patience, practice, and the use of various learning methods, including visual aids, interactive exercises, and games.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to calculate 25 x 10?
A: The quickest way is to add a zero to the end of 25, resulting in 250. This is a direct application of the shortcut for multiplying by powers of 10.
Q: Can I use a calculator to solve 25 x 10?
A: Yes, a calculator can be used, but understanding the underlying principles is crucial for developing mathematical proficiency.
Q: What if I need to calculate 25 x 11 instead of 25 x 10?
A: You can use the distributive property: 25 x (10 + 1) = (25 x 10) + (25 x 1) = 250 + 25 = 275. Alternatively, you can perform the standard multiplication algorithm.
Q: How does this relate to algebra?
A: In algebra, you might see expressions like 25x where 'x' represents a variable. If x = 10, then 25x would evaluate to 250. This demonstrates the extension of basic arithmetic principles to symbolic representations.
Conclusion: More Than Just an Answer
The seemingly simple question, "What is 25 x 10?", provides a gateway to explore fundamental mathematical concepts, problem-solving strategies, and practical applications. While the answer is 250, the journey to understanding the underlying principles is far more valuable. Mastering multiplication lays a strong foundation for more advanced mathematical concepts and contributes to success in numerous fields. By understanding different methods and appreciating the interconnectedness of mathematical operations, we can unlock a deeper appreciation for the beauty and utility of mathematics in our daily lives. The ability to effortlessly solve problems like 25 x 10 is not just about finding the correct answer; it's about developing a solid mathematical foundation that will serve you well throughout your life.
Latest Posts
Latest Posts
-
134 Degrees F To K
Sep 22, 2025
-
3 25 Percent As A Decimal
Sep 22, 2025
-
Lcm For 14 And 21
Sep 22, 2025
-
12 5 Is An Improper Fraction
Sep 22, 2025
-
75 Of 48 Is What
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.