What Is 9 X 6
horsecheck
Sep 22, 2025 · 6 min read
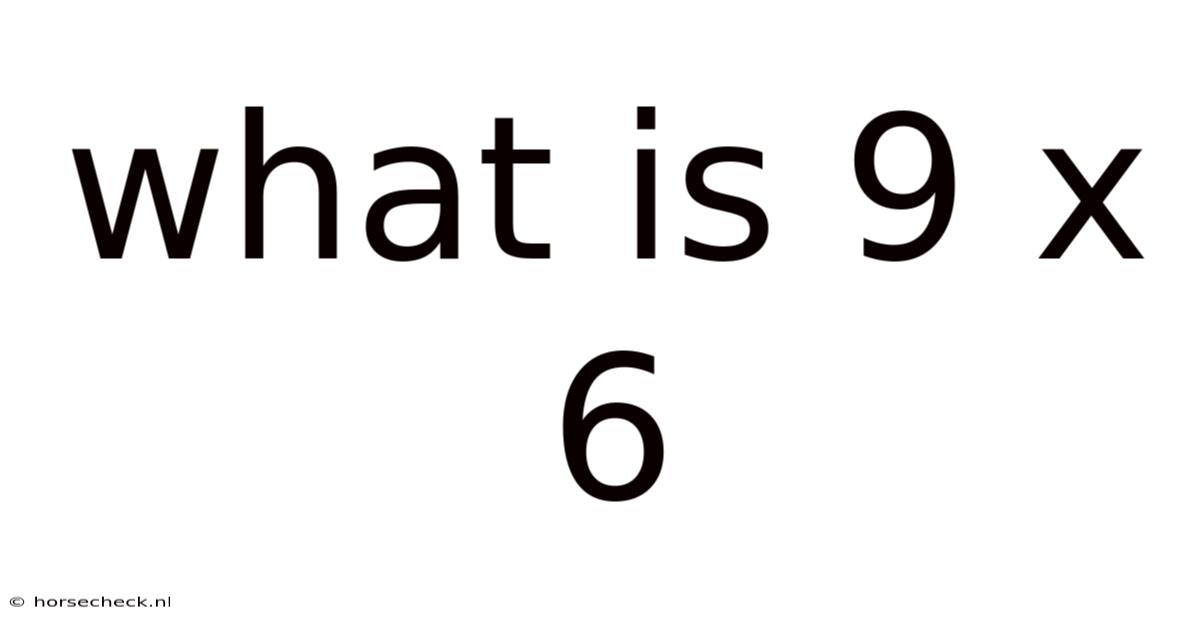
Table of Contents
What is 9 x 6? A Deep Dive into Multiplication and Beyond
What is 9 x 6? The seemingly simple question hides a universe of mathematical concepts, from basic arithmetic to advanced algebraic principles. This article will not only answer the question definitively but will also explore the underlying principles of multiplication, its various applications, and its significance in broader mathematical contexts. We'll delve into different methods of solving this equation, explore the history of multiplication, and even touch upon its role in more complex mathematical fields. By the end, you'll not only know that 9 x 6 = 54, but you'll also understand why it's true and how this seemingly simple calculation underpins much of the world around us.
Understanding Multiplication: The Foundation of 9 x 6
Multiplication, at its core, is repeated addition. When we say 9 x 6, we're essentially asking: what is the sum of nine sixes? This can be visualized in several ways:
- Repeated Addition: 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 54
- Arrays: Imagine a rectangular array with 9 rows and 6 columns. Counting the total number of squares gives you the answer, 54.
- Number Line: Jumping six units on a number line nine times will also lead to 54.
These visual representations are crucial, especially for younger learners, as they provide a concrete understanding of the abstract concept of multiplication. They help to bridge the gap between concrete objects and abstract mathematical ideas. The ability to visualize multiplication significantly improves comprehension and retention.
Methods for Solving 9 x 6
While the repeated addition method works, it's not the most efficient for larger numbers. Let's explore other methods to solve 9 x 6:
- Multiplication Table: The most common approach is using a multiplication table. Memorizing multiplication tables is a cornerstone of elementary math education. Learning the tables provides a quick and efficient way to recall multiplication facts. Simply locating the intersection of the 9th row and the 6th column gives us 54.
- Distributive Property: This powerful property allows us to break down a multiplication problem into smaller, easier-to-manage parts. We can rewrite 9 x 6 as (10 - 1) x 6. Using the distributive property, this becomes (10 x 6) - (1 x 6) = 60 - 6 = 54. This method is particularly useful when dealing with numbers close to multiples of 10.
- Factors and Prime Factorization: Breaking down numbers into their prime factors can also be helpful. 9 can be factored into 3 x 3, and 6 can be factored into 2 x 3. Therefore, 9 x 6 = (3 x 3) x (2 x 3) = 2 x 3 x 3 x 3 = 54. This approach highlights the fundamental building blocks of numbers and their relationships.
- Visual Aids: Diagrams, such as arrays or area models, provide a visual representation of the multiplication problem. Drawing a 9 x 6 rectangle and dividing it into smaller squares can help visualize the total number of squares, leading to the answer 54. This method is especially helpful for kinesthetic learners.
The Significance of 9 x 6 in Broader Mathematical Contexts
While 9 x 6 = 54 might seem like a simple calculation, its implications extend far beyond basic arithmetic. Understanding multiplication is crucial for:
- Algebra: Multiplication is a fundamental operation in algebra. It's used to solve equations, simplify expressions, and understand relationships between variables. Concepts like distributive property and factoring, which we touched upon earlier, are central to algebraic manipulation.
- Geometry: Calculating areas and volumes often involves multiplication. For instance, the area of a rectangle is length times width. To find the area of a rectangle with sides 9 units and 6 units, we'd use the equation 9 x 6 = 54 square units.
- Calculus: While seemingly far removed from basic multiplication, calculus relies heavily on the concept of limits, which often involve increasingly fine-grained divisions and multiplications. The fundamental theorem of calculus connects differentiation and integration, both of which rely on the principles of multiplication and addition.
- Data Analysis and Statistics: Multiplication plays a vital role in statistical calculations, particularly when dealing with probabilities, proportions, and scaling data. Understanding proportions often requires manipulating fractions, which itself necessitates a strong grasp of multiplication and division.
- Everyday Life: From calculating the total cost of items (e.g., 9 items at $6 each), to figuring out the distance traveled (e.g., 9 hours at 6 miles per hour), multiplication is essential for navigating our daily lives.
Historical Context of Multiplication
The concept of multiplication has ancient roots. Evidence suggests that various civilizations, including the Egyptians, Babylonians, and Greeks, developed methods of multiplication centuries ago. However, the notation and algorithms we use today evolved over time, with significant contributions from mathematicians across different cultures and eras. The development of the Hindu-Arabic numeral system, with its place value system, revolutionized the way we perform multiplication, making it significantly more efficient than previous methods. The development of algorithms like the lattice method further enhanced the efficiency and accuracy of multiplication.
Frequently Asked Questions (FAQs)
Q: What are some common mistakes people make when multiplying?
A: Common mistakes include errors in carrying over digits, misplacing decimal points (in decimal multiplication), and incorrectly applying the order of operations (PEMDAS/BODMAS). Practicing regularly and carefully checking work helps to minimize errors.
Q: How can I improve my multiplication skills?
A: Consistent practice is key. Use flashcards, online games, and worksheets to reinforce multiplication facts. Try different methods of multiplication to find one that suits your learning style. Understanding the underlying principles—repeated addition, distributive property, etc.—will enhance your comprehension and problem-solving abilities.
Q: Is there a shortcut to multiplying by 9?
A: Yes! One trick is to multiply the number by 10 and then subtract the original number. For example, 9 x 6 = (10 x 6) - 6 = 60 - 6 = 54.
Q: Why is memorizing multiplication tables important?
A: Memorizing multiplication tables significantly improves calculation speed and efficiency. It frees up mental resources, allowing you to focus on more complex problems. It's a fundamental building block for more advanced mathematical concepts.
Conclusion: Beyond 9 x 6
We started with a seemingly simple question: What is 9 x 6? The answer, 54, is just the tip of the iceberg. This article explored the diverse facets of multiplication, highlighting its importance in various mathematical domains and its relevance in everyday life. Understanding multiplication is not just about getting the right answer; it's about grasping the underlying principles and appreciating its power as a fundamental building block of mathematics and beyond. By exploring different methods and understanding its historical context, we gain a richer appreciation for this seemingly simple, yet incredibly powerful, mathematical operation. The journey from understanding 9 x 6 to grasping its broader implications underscores the beauty and interconnectedness of mathematics. Keep exploring, keep learning, and the world of numbers will continue to reveal its fascinating secrets.
Latest Posts
Latest Posts
-
40c Is What In F
Sep 22, 2025
-
What Is 1 3 9
Sep 22, 2025
-
What Is 1 4 Of 40
Sep 22, 2025
-
What Is 75 Of 84
Sep 22, 2025
-
What Is 5 Of 11
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.