What Is Equal To 2/3
horsecheck
Sep 22, 2025 · 6 min read
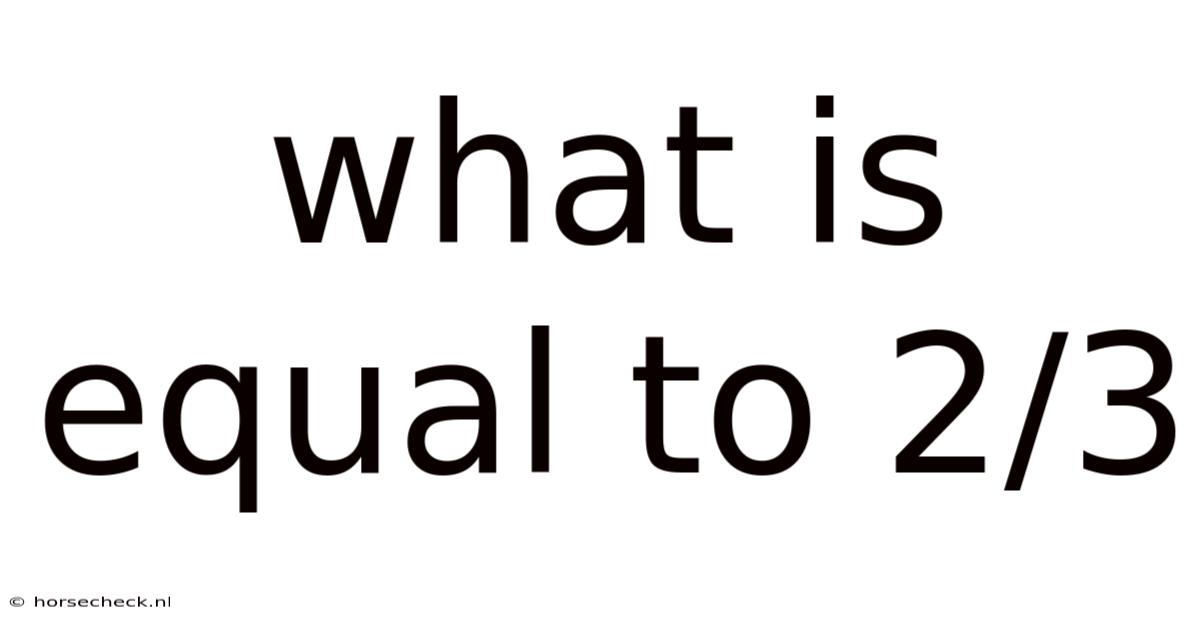
Table of Contents
Decoding the Fraction: What is Equal to 2/3? A Comprehensive Guide
What is equal to 2/3? This seemingly simple question opens a door to a deeper understanding of fractions, equivalent fractions, decimals, percentages, and even ratios. This comprehensive guide will explore various ways to represent the fraction 2/3, delve into the mathematical concepts behind it, and provide practical applications. We'll cover everything from finding equivalent fractions to converting 2/3 into decimals and percentages, ensuring you grasp the concept thoroughly.
Understanding Fractions: A Quick Refresher
Before we dive into the equivalents of 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have. In 2/3, the numerator is 2.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into. In 2/3, the denominator is 3.
Therefore, 2/3 means we have 2 parts out of a total of 3 equal parts.
Finding Equivalent Fractions: The Key to Understanding 2/3
Equivalent fractions represent the same value even though they look different. They are created by multiplying or dividing both the numerator and the denominator by the same non-zero number. This doesn't change the fundamental value of the fraction; it simply expresses it in a different form.
To find equivalent fractions for 2/3, we can multiply both the numerator and the denominator by the same number:
- Multiply by 2: (2 x 2) / (3 x 2) = 4/6
- Multiply by 3: (2 x 3) / (3 x 3) = 6/9
- Multiply by 4: (2 x 4) / (3 x 4) = 8/12
- Multiply by 5: (2 x 5) / (3 x 5) = 10/15
- And so on...
We can generate an infinite number of equivalent fractions for 2/3 by continuing this process. All these fractions – 4/6, 6/9, 8/12, 10/15, and countless others – are equal to 2/3. They all represent the same portion of a whole.
Simplifying Fractions: Finding the Simplest Form
While we can create numerous equivalent fractions, it's often helpful to express a fraction in its simplest form. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
In the case of 2/3, the GCD of 2 and 3 is 1. Since dividing both by 1 doesn't change the values, 2/3 is already in its simplest form. This is a key concept to remember – sometimes, the fraction you start with is already the simplest representation.
Converting 2/3 to a Decimal: Division is Key
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 2/3:
2 ÷ 3 = 0.66666...
This results in a repeating decimal, often represented as 0.6̅. The bar above the 6 indicates that the digit 6 repeats infinitely. This is a characteristic of many fractions; they don't always translate neatly into terminating decimals.
Converting 2/3 to a Percentage: From Decimal to Percentage
Converting a decimal to a percentage is straightforward: multiply the decimal by 100 and add the percent sign (%).
0.66666... x 100 ≈ 66.67%
Again, we encounter a repeating decimal, leading to an approximate percentage value. We commonly round repeating decimals to a reasonable number of decimal places for practical applications.
Visualizing 2/3: Pictorial Representations
Understanding fractions can be greatly enhanced by visualizing them. Consider a circle divided into three equal parts. If two of those parts are shaded, this visually represents the fraction 2/3. This visual approach helps solidify the concept and makes the abstract idea more concrete. Similarly, imagine a rectangle divided into three equal columns; shading two of them also depicts 2/3.
Real-world Applications of 2/3
The fraction 2/3 appears frequently in various real-world scenarios:
- Cooking: A recipe might call for 2/3 cup of sugar.
- Measurements: Determining lengths or distances can involve fractions like 2/3 of a meter.
- Probability: Calculating the likelihood of an event might result in a probability of 2/3.
- Data Analysis: Representing proportions or ratios within datasets.
Understanding how to work with 2/3 is crucial for tackling these everyday problems.
Working with 2/3 in Calculations: Addition, Subtraction, Multiplication, and Division
Let's explore how to perform basic arithmetic operations with 2/3:
Addition: To add fractions, they need a common denominator. For example, adding 2/3 and 1/2:
Find a common denominator (6): (2/3) x (2/2) = 4/6; (1/2) x (3/3) = 3/6 Add the numerators: 4/6 + 3/6 = 7/6 = 1 1/6
Subtraction: Similar to addition, subtraction requires a common denominator:
Subtracting 1/3 from 2/3: 2/3 - 1/3 = 1/3
Multiplication: Multiply the numerators together and the denominators together:
Multiplying 2/3 by 1/2: (2 x 1) / (3 x 2) = 2/6 = 1/3
Division: Invert the second fraction (reciprocal) and multiply:
Dividing 2/3 by 1/2: (2/3) x (2/1) = 4/3 = 1 1/3
Advanced Concepts: Ratios and Proportions
The fraction 2/3 can also be expressed as a ratio: 2:3. This ratio represents the relationship between two quantities. Understanding ratios and proportions is fundamental in many fields, including scaling recipes, mixing solutions, and solving geometric problems. For example, if you have a ratio of 2:3, and you know one quantity is 6, you can solve for the other quantity using proportions.
Frequently Asked Questions (FAQ)
Q: Is 2/3 a rational number?
A: Yes, 2/3 is a rational number because it can be expressed as a fraction of two integers (2 and 3).
Q: Can 2/3 be expressed as a mixed number?
A: No, 2/3 is already in its simplest form. It's a proper fraction (numerator < denominator). To express it as a mixed number, you'd have to add a whole number, and this would change its value.
Q: What is the reciprocal of 2/3?
A: The reciprocal of 2/3 is 3/2 (or 1.5).
Q: How do I compare 2/3 to other fractions?
A: Convert all fractions to equivalent fractions with a common denominator to easily compare their values.
Q: Are there any other ways to represent 2/3 besides decimals and percentages?
A: Yes, you can represent 2/3 visually using diagrams, charts, or even physical objects to represent parts of a whole.
Conclusion: Mastering the Fraction 2/3
Understanding what is equal to 2/3 involves a broader grasp of fractional concepts, including equivalent fractions, decimal conversions, percentage representations, and their applications in real-world scenarios. By mastering these concepts, you gain a valuable skill applicable in various fields, from cooking and construction to advanced mathematics and data analysis. Remember, practice is key to solidifying your understanding of fractions. Start by working through examples, visualizing the fractions, and applying them in practical exercises. The more you practice, the more comfortable you will become with working with fractions like 2/3 and beyond.
Latest Posts
Latest Posts
-
What Is 1 3 9
Sep 22, 2025
-
What Is 1 4 Of 40
Sep 22, 2025
-
What Is 75 Of 84
Sep 22, 2025
-
What Is 5 Of 11
Sep 22, 2025
-
Write 2 5 As A Decimal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is Equal To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.