0.003 Is 1 10 Of
horsecheck
Sep 25, 2025 · 5 min read
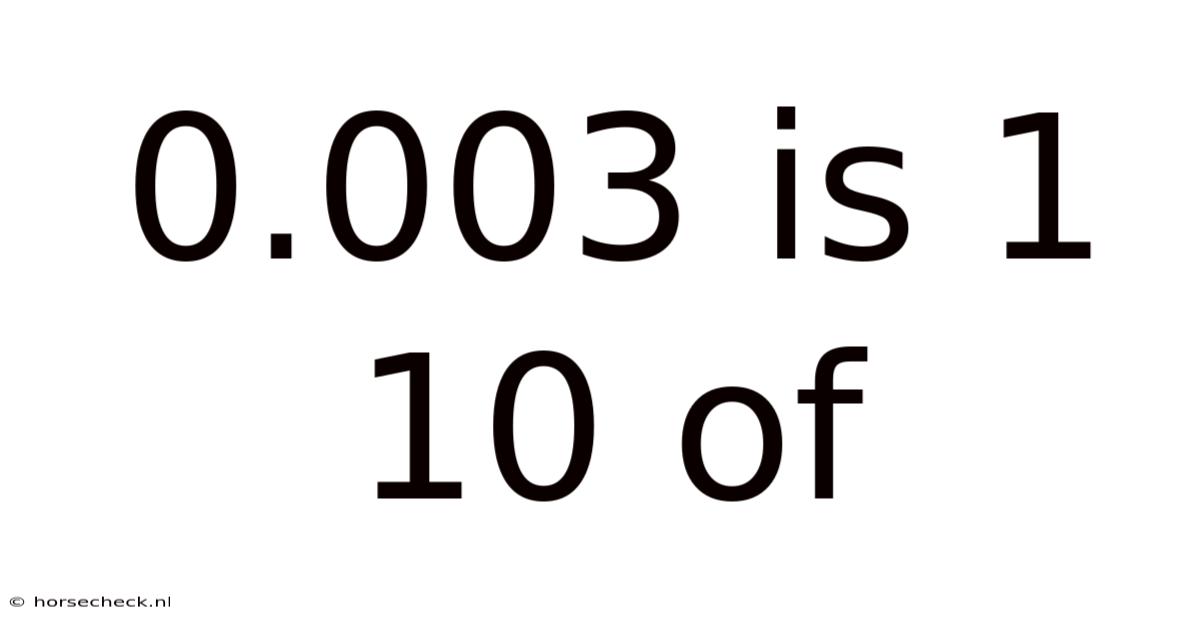
Table of Contents
Decoding 0.003: Understanding its Relationship to 1/10th
The statement "0.003 is 1/10 of..." is incomplete. It's a riddle of sorts, prompting us to explore the relationship between the decimal 0.003 and a tenth (1/10 or 0.1). This exploration will delve into the world of decimals, fractions, and proportional reasoning, offering a deeper understanding of how these mathematical concepts interconnect. Understanding this relationship is fundamental to various fields, from basic arithmetic to advanced calculations in science and engineering.
Understanding Decimals and Fractions
Before we tackle the core question, let's solidify our understanding of decimals and fractions. Both represent parts of a whole. A fraction expresses a part as a ratio of two integers (numerator and denominator), while a decimal expresses a part as a base-10 number system, using a decimal point to separate the whole number from the fractional part.
For instance, the fraction 1/10 represents one part out of ten equal parts. Its decimal equivalent is 0.1. Similarly, 1/100 is 0.01, and 1/1000 is 0.001. These examples demonstrate the direct relationship between fractions with a denominator that is a power of 10 and their decimal counterparts.
Finding the Whole: The Missing Piece of the Puzzle
The statement "0.003 is 1/10 of..." implies that 0.003 is one-tenth of a larger number. To find this larger number, we need to perform a simple calculation. Since 0.003 represents 1/10 of the unknown number, we can multiply 0.003 by 10 to find the original value:
0.003 * 10 = 0.03
Therefore, 0.003 is 1/10 of 0.03.
Expanding the Understanding: Proportional Reasoning
This seemingly simple calculation highlights the importance of proportional reasoning. Proportional reasoning is the ability to understand and use the relationships between quantities. It allows us to solve problems involving ratios and proportions, which are fundamental to many areas of mathematics and beyond.
In this case, we used a simple proportion:
0.003 / x = 1/10
Where 'x' represents the unknown number. Solving for 'x' involves cross-multiplication:
0.003 * 10 = 1 * x 0.03 = x
This confirms our earlier calculation.
Visualizing the Relationship: A Practical Approach
To further solidify our understanding, let's visualize the relationship between 0.003 and 0.03. Imagine a meter stick divided into 1000 equal parts (millimeters).
- 0.003 would represent 3 millimeters on the meter stick.
- 0.03 would represent 30 millimeters (ten times the length of 0.003).
This visual representation clearly illustrates that 0.003 is indeed one-tenth of 0.03.
Beyond the Basics: Applying the Concept
The concept of finding a whole from a fraction extends far beyond this simple example. It finds applications in various real-world scenarios:
- Percentage Calculations: Calculating percentages involves similar proportional reasoning. For example, if 0.003 represents 1% of a quantity, we can find the total quantity by multiplying 0.003 by 100.
- Scaling and Measurement: In engineering and architecture, scaling drawings involves proportional relationships. A small model representing a large structure utilizes similar principles.
- Financial Calculations: Interest calculations, loan repayments, and other financial computations often rely on proportional reasoning to determine future values based on a given rate.
- Scientific Data Analysis: In scientific experiments, researchers frequently analyze data involving ratios and proportions to draw conclusions and make predictions.
Understanding Different Representations: Fractions, Decimals, and Percentages
It's crucial to be comfortable converting between fractions, decimals, and percentages. This flexibility enhances problem-solving capabilities.
Let's consider our example:
- Fraction: 0.003 can be expressed as 3/1000.
- Decimal: 0.003 is already in decimal form.
- Percentage: 0.003 can be expressed as 0.3% (0.003 * 100%).
Understanding these interchangeable representations helps in choosing the most appropriate format for a given problem.
Further Exploration: Working with More Complex Problems
Let's extend the concept to more intricate scenarios. Suppose we know that 0.003 is 1/20 of a certain number. How would we find that number?
We can set up a proportion:
0.003 / x = 1/20
Cross-multiplying:
0.003 * 20 = 1 * x 0.06 = x
Therefore, 0.003 is 1/20 of 0.06. This shows the adaptable nature of proportional reasoning to various fractional relationships.
Frequently Asked Questions (FAQ)
Q1: How can I easily convert fractions to decimals?
A1: To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, 1/4 = 1 ÷ 4 = 0.25.
Q2: How can I easily convert decimals to percentages?
A2: To convert a decimal to a percentage, multiply the decimal by 100 and add a percentage sign (%). For example, 0.25 = 0.25 * 100% = 25%.
Q3: What if the denominator of a fraction isn't a power of 10?
A3: If the denominator isn't a power of 10, you can either perform long division to obtain the decimal equivalent or find an equivalent fraction with a denominator that is a power of 10.
Q4: Are there any online tools to help with these conversions?
A4: Yes, many online calculators and converters are available that can assist with converting between fractions, decimals, and percentages.
Conclusion: Mastering Proportional Reasoning
Understanding the relationship between 0.003 and 1/10th, and more broadly, mastering proportional reasoning, is a cornerstone of mathematical proficiency. It's a skill applicable across diverse fields, from everyday calculations to complex scientific and engineering applications. By practicing different types of problems and employing different representations (fractions, decimals, percentages), one can build a solid foundation in this critical mathematical concept. Remember, the key is to understand the underlying principles and apply them flexibly to a wide range of situations. The seemingly simple question, "0.003 is 1/10 of...", opens the door to a rich understanding of mathematical relationships and their profound impact on various aspects of life.
Latest Posts
Latest Posts
-
3 1 6 As A Fraction
Sep 25, 2025
-
1 3 A 5 4
Sep 25, 2025
-
Is 110 A Perfect Square
Sep 25, 2025
-
34 8 As A Mixed Number
Sep 25, 2025
-
2 3 In A Number
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 0.003 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.