2 1/6 As A Fraction
horsecheck
Sep 24, 2025 · 6 min read
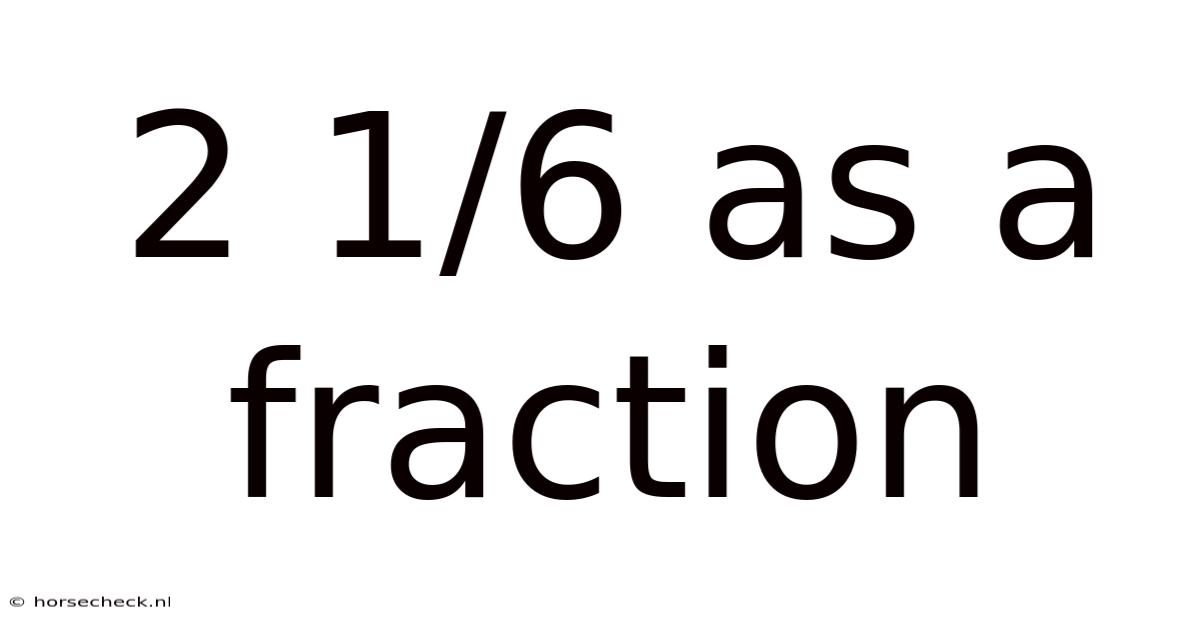
Table of Contents
Understanding 2 1/6 as a Fraction: A Comprehensive Guide
Are you struggling with mixed numbers and improper fractions? Understanding how to represent numbers like 2 1/6 as a single fraction is a fundamental skill in mathematics. This comprehensive guide will walk you through the process, explaining the concepts in detail and providing examples to solidify your understanding. We'll cover converting mixed numbers to improper fractions, simplifying fractions, and even explore the practical applications of this knowledge. By the end, you'll be confident in handling mixed numbers and their fractional equivalents.
What is a Mixed Number?
A mixed number combines a whole number and a fraction. For example, 2 1/6 represents two whole units and one-sixth of another unit. While useful for visualizing quantities, mixed numbers can be less practical for mathematical operations like addition and multiplication. That's where converting to an improper fraction comes in handy.
What is an Improper Fraction?
An improper fraction has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). Unlike a mixed number, an improper fraction represents a quantity greater than or equal to one whole unit. Converting 2 1/6 to an improper fraction is the key to making it easier to work with mathematically.
Converting 2 1/6 to an Improper Fraction: A Step-by-Step Guide
The conversion process involves two simple steps:
-
Multiply the whole number by the denominator: In our example, the whole number is 2, and the denominator is 6. 2 multiplied by 6 equals 12.
-
Add the numerator: Now, add the numerator of the fraction (1) to the result from step 1 (12). 12 + 1 = 13. This sum becomes the new numerator of our improper fraction.
-
Keep the denominator the same: The denominator of the improper fraction remains the same as the denominator of the original mixed number, which is 6.
Therefore, 2 1/6 as an improper fraction is 13/6.
Let's illustrate this with another example: Convert 3 2/5 to an improper fraction.
- Multiply the whole number by the denominator: 3 x 5 = 15
- Add the numerator: 15 + 2 = 17
- Keep the denominator the same: The denominator remains 5.
So, 3 2/5 as an improper fraction is 17/5.
Why Convert to Improper Fractions?
Converting mixed numbers to improper fractions simplifies many mathematical operations. Consider adding two mixed numbers: 2 1/6 + 1 2/6. While possible to add them directly, it's often easier to convert them to improper fractions first:
- 2 1/6 = 13/6
- 1 2/6 = 8/6
Now, adding the improper fractions is straightforward: 13/6 + 8/6 = 21/6. Then, you can convert this improper fraction back to a mixed number if needed: 21/6 = 3 3/6 = 3 1/2.
Simplifying Fractions
Once you have an improper fraction, it's often helpful to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's simplify 21/6:
-
Find the GCD of 21 and 6: The factors of 21 are 1, 3, 7, and 21. The factors of 6 are 1, 2, 3, and 6. The greatest common factor is 3.
-
Divide both the numerator and denominator by the GCD: 21 ÷ 3 = 7 and 6 ÷ 3 = 2.
Therefore, the simplified form of 21/6 is 7/2. This is still an improper fraction, but it's in its simplest form. We can then convert it back to a mixed number: 7/2 = 3 1/2.
Converting Improper Fractions Back to Mixed Numbers
To convert an improper fraction back to a mixed number, you perform the reverse operation:
-
Divide the numerator by the denominator: For example, let's convert 7/2 back to a mixed number. 7 divided by 2 is 3 with a remainder of 1.
-
The quotient becomes the whole number: The quotient (3) becomes the whole number part of the mixed number.
-
The remainder becomes the numerator: The remainder (1) becomes the numerator of the fraction.
-
The denominator stays the same: The denominator (2) remains unchanged.
Therefore, 7/2 as a mixed number is 3 1/2.
Practical Applications of Converting Mixed Numbers and Improper Fractions
Understanding the conversion between mixed numbers and improper fractions is crucial in various mathematical contexts:
- Adding and subtracting fractions: As demonstrated earlier, converting to improper fractions simplifies these operations.
- Multiplying and dividing fractions: While not strictly necessary, converting to improper fractions can make these operations easier to visualize and calculate.
- Working with measurements: In fields like cooking, construction, and engineering, precise measurements often involve fractions, and understanding mixed numbers and improper fractions is essential for accurate calculations.
- Solving algebraic equations: Many algebraic equations involve fractions, and the ability to work with mixed numbers and improper fractions is necessary for finding solutions.
Frequently Asked Questions (FAQ)
Q: Can all mixed numbers be converted to improper fractions?
A: Yes, absolutely. Every mixed number has a corresponding improper fraction representation.
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, every improper fraction can be converted to a mixed number (except for fractions where the numerator is equal to the denominator, which equals 1).
Q: Is there only one way to represent a given quantity as a fraction?
A: No, a given quantity can be represented by many equivalent fractions. For example, 1/2 is equivalent to 2/4, 3/6, and so on. However, there is only one simplified improper fraction and one simplified mixed number for any given quantity.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to work with and understand. It also ensures consistency in calculations and presentations.
Q: What if I encounter a very large mixed number?
A: The conversion process remains the same, regardless of the size of the whole number. Simply follow the steps outlined above, and you will be able to convert even the largest mixed numbers to their equivalent improper fractions.
Conclusion
Converting 2 1/6 to an improper fraction (13/6) and understanding the broader concepts of mixed numbers and improper fractions are essential skills for anyone studying mathematics. This skill is not just about manipulating numbers; it's about developing a deeper understanding of how fractions represent parts of a whole and how to represent quantities in different but equivalent forms. By mastering this conversion, you'll build a strong foundation for more advanced mathematical concepts and real-world applications. Remember the simple steps, practice regularly with different examples, and you'll quickly become proficient in working with mixed numbers and improper fractions. This understanding will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Whats 0 3 As A Fraction
Sep 24, 2025
-
Simplest Form Of 4 5
Sep 24, 2025
-
Percent Of 4 Is 7
Sep 24, 2025
-
6 4 As A Decimal
Sep 24, 2025
-
Hcf Of 3 And 5
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 1/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.