55/12 As A Mixed Number
horsecheck
Sep 22, 2025 · 5 min read
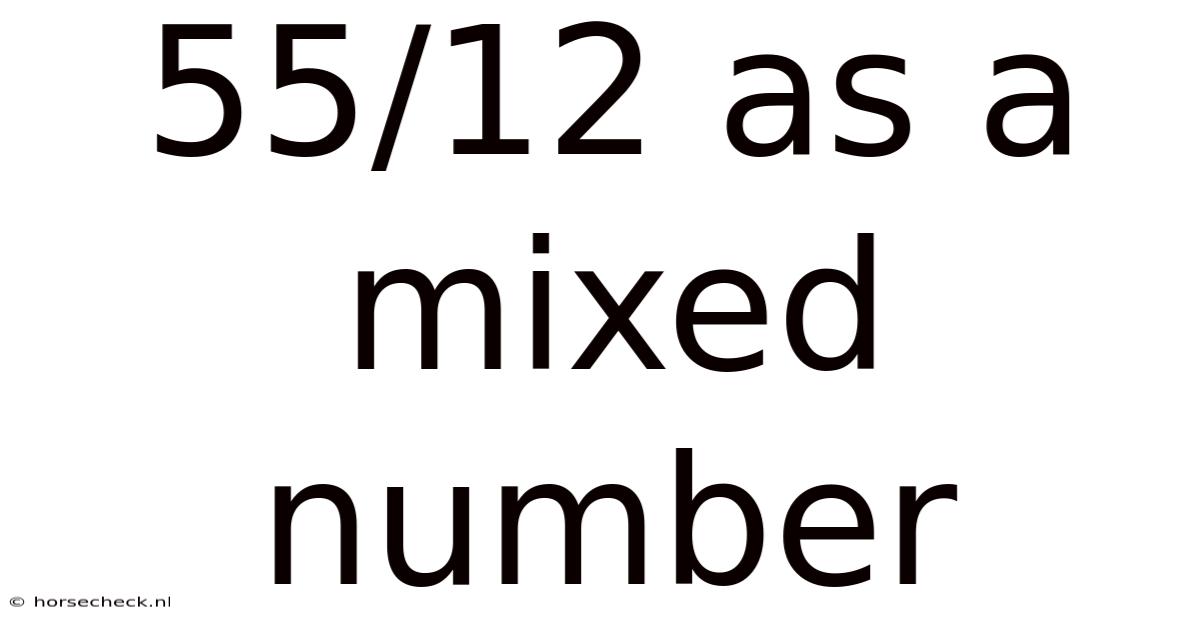
Table of Contents
55/12 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 55/12 into a mixed number, explaining the steps involved and providing a deeper understanding of the underlying concepts. We'll explore various methods, address common questions, and even touch upon the practical applications of this conversion. This guide is perfect for students learning about fractions, teachers looking for supplementary teaching materials, or anyone wishing to refresh their knowledge of basic arithmetic.
Understanding Fractions and Mixed Numbers
Before diving into the conversion, let's clarify the definitions of improper fractions and mixed numbers.
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Our example, 55/12, is an improper fraction because 55 > 12.
-
Mixed Number: A mixed number is a combination of a whole number and a proper fraction. A proper fraction is one where the numerator is less than the denominator. For example, 2 ¾ is a mixed number.
Converting an improper fraction like 55/12 to a mixed number involves finding out how many times the denominator (12) goes into the numerator (55) and expressing the remainder as a fraction.
Method 1: Long Division
The most straightforward method to convert 55/12 into a mixed number is through long division.
-
Divide the numerator by the denominator: Divide 55 by 12.
4 12 | 55 -48 7 -
Identify the whole number: The quotient (the result of the division) is 4. This is the whole number part of our mixed number.
-
Identify the remainder: The remainder is 7. This becomes the numerator of the fractional part of our mixed number.
-
Form the mixed number: The denominator remains the same (12). Therefore, 55/12 as a mixed number is 4 7/12.
Method 2: Repeated Subtraction
This method is a bit more intuitive and helpful for visualizing the process.
-
Subtract the denominator from the numerator repeatedly: Subtract 12 from 55 until the result is less than 12.
- 55 - 12 = 43
- 43 - 12 = 31
- 31 - 12 = 19
- 19 - 12 = 7
-
Count the subtractions: We subtracted 12 four times. This is our whole number (4).
-
The remaining number is the remainder: The remaining number after the repeated subtractions is 7. This becomes the numerator of our fraction.
-
Form the mixed number: The denominator remains 12. Therefore, 55/12 as a mixed number is 4 7/12.
Method 3: Understanding the Concept of Division
This method focuses on the conceptual understanding of what a fraction represents. The fraction 55/12 signifies 55 parts out of a total of 12 parts. Each set of 12 parts constitutes a whole.
-
Determine the number of wholes: We can determine how many complete sets of 12 we have in 55. Through division (or repeated subtraction), we find that we have four complete sets of 12 (4 x 12 = 48).
-
Calculate the remaining parts: After taking out four sets of 12, we have 55 - 48 = 7 parts remaining.
-
Form the mixed number: These 7 remaining parts, out of a possible 12, are represented as 7/12. Therefore, the mixed number is 4 7/12.
Visual Representation
Imagine you have 55 pizzas, and you want to divide them equally among 12 friends. Each friend would get 4 whole pizzas (4 x 12 = 48 pizzas). You'd have 7 pizzas left over (55 - 48 = 7). These 7 pizzas represent the remaining fraction, 7/12, of a pizza per friend.
Simplifying the Fraction (if possible)
In our example, the fraction 7/12 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and the denominator is 1. In this case, the GCD of 7 and 12 is 1, meaning the fraction cannot be simplified further. However, it's always a good practice to check for simplification.
Practical Applications
Converting improper fractions to mixed numbers is crucial in various real-world applications:
-
Cooking and Baking: Recipes often use mixed numbers for ingredient measurements.
-
Construction and Engineering: Measurements and calculations frequently involve mixed numbers.
-
Everyday Measurements: Working with lengths, weights, and volumes often requires converting between improper fractions and mixed numbers.
Frequently Asked Questions (FAQ)
Q: Why is it important to convert improper fractions to mixed numbers?
A: Mixed numbers are often easier to understand and visualize than improper fractions. They provide a clearer representation of quantities involving whole units and parts of a unit.
Q: Can all improper fractions be converted into mixed numbers?
A: Yes, all improper fractions can be converted into mixed numbers. The process involves dividing the numerator by the denominator.
Q: What if the remainder is zero after the division?
A: If the remainder is zero, it means the improper fraction is a whole number. For example, 24/6 = 4. There's no fractional part.
Q: Are there any other methods to convert improper fractions to mixed numbers?
A: While the methods described above are the most common and straightforward, other methods might exist depending on the specific context or mathematical approach. The core principle remains the same: divide the numerator by the denominator to find the whole number and the remainder to form the fractional part.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various examples, try different methods, and visualize the concepts. Using manipulatives (like fraction circles or blocks) can also help improve understanding.
Conclusion
Converting the improper fraction 55/12 to a mixed number results in 4 7/12. We explored three different methods to achieve this conversion: long division, repeated subtraction, and a conceptual understanding of division. This process is essential in various mathematical contexts and real-world applications. Understanding these methods not only helps you solve this specific problem but builds a stronger foundation in fraction arithmetic. Remember to always check if the resulting fraction can be simplified further to its lowest terms. With continued practice and a firm grasp of the underlying principles, you'll find working with fractions increasingly intuitive and straightforward.
Latest Posts
Latest Posts
-
19 26 As A Percentage
Sep 22, 2025
-
2 3 Repeating As A Fraction
Sep 22, 2025
-
What Percent Is 29 34
Sep 22, 2025
-
What Is 1 3 4 5
Sep 22, 2025
-
What Is 20 Of 37 00
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 55/12 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.