62 100 As A Percentage
horsecheck
Sep 25, 2025 · 5 min read
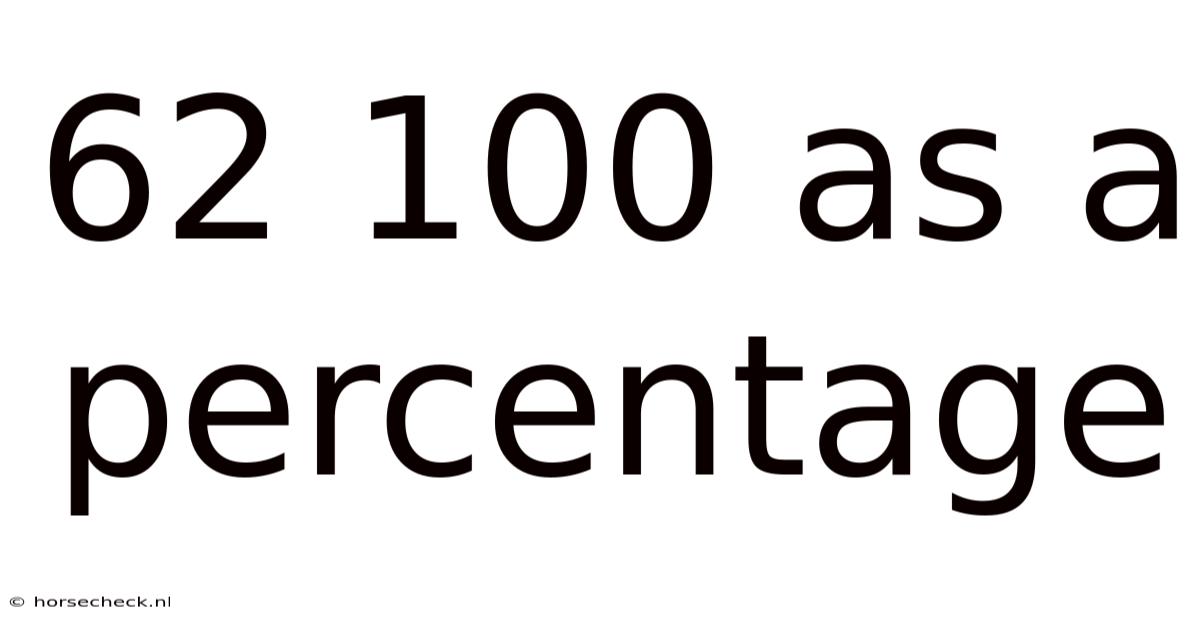
Table of Contents
62 out of 100 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to analyzing data and understanding statistics. This article will thoroughly explore how to express 62 out of 100 as a percentage, providing a detailed explanation, various methods for calculation, real-world examples, and addressing common questions. We'll also delve into the broader context of percentage calculations to solidify your understanding.
Understanding Percentages: A Quick Refresher
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent"). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to compare proportions and make calculations easier to understand.
Calculating 62 out of 100 as a Percentage: The Basic Method
The simplest method to calculate 62 out of 100 as a percentage involves a straightforward formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 62
- Whole: 100
Substituting these values into the formula:
(62 / 100) * 100% = 62%
Therefore, 62 out of 100 is 62%.
Alternative Methods for Calculating Percentages
While the above method is the most direct, there are other approaches that can be helpful depending on the context:
-
Using Proportions: You can set up a proportion to solve for the percentage. For example:
x/100 = 62/100
Solving for x, we get x = 62. Therefore, 62 out of 100 is 62%. This method is particularly useful when dealing with proportions where the whole is not 100.
-
Using Decimal Conversion: You can first convert the fraction 62/100 into a decimal by dividing 62 by 100, which equals 0.62. Then, multiply the decimal by 100% to obtain the percentage: 0.62 * 100% = 62%.
-
Mental Calculation: In this specific case, since the denominator is 100, the calculation is quite simple. The numerator directly represents the percentage.
Real-World Applications of Percentage Calculations: Examples
Understanding percentages is crucial in various real-life scenarios:
-
Academic Performance: If a student scores 62 out of 100 on a test, their score is 62%. This allows for easy comparison with other students' scores.
-
Sales and Discounts: A store offering a 62% discount on an item means the price reduction is 62% of the original price.
-
Financial Analysis: Businesses use percentages to analyze profit margins, growth rates, and other key financial metrics. A 62% increase in sales, for instance, indicates substantial growth.
-
Data Representation: Percentages are used extensively in charts and graphs to visually represent proportions of data, making complex information more accessible.
-
Surveys and Polls: Results from surveys and polls are often expressed as percentages to show the proportion of respondents who chose a particular option. For example, 62% of respondents might favor a specific political candidate.
-
Interest Rates and Loans: Interest rates on loans and savings accounts are expressed as percentages. Understanding these percentages is essential for making informed financial decisions.
Beyond 62 out of 100: Calculating Percentages with Different Numerators and Denominators
The method of (Part / Whole) * 100% remains the core principle even when the denominator isn't 100. For instance, let's say you scored 45 out of 75 on a quiz:
(45 / 75) * 100% = 60%
In this case, your score is 60%.
Similarly, if you have 30 successes out of 50 attempts, the success rate is:
(30 / 50) * 100% = 60%
Working with Percentages: Increasing and Decreasing Values
Percentages are also used to calculate increases and decreases in values.
Increase: To increase a value by a certain percentage, you multiply the value by (1 + percentage/100). For example, to increase 200 by 10%, you would calculate:
200 * (1 + 10/100) = 200 * 1.10 = 220
Decrease: To decrease a value by a certain percentage, you multiply the value by (1 - percentage/100). To decrease 200 by 10%, you would calculate:
200 * (1 - 10/100) = 200 * 0.90 = 180
Frequently Asked Questions (FAQs)
Q1: What is the simplest way to remember how to calculate percentages?
A1: Remember the basic formula: (Part / Whole) * 100% = Percentage. This formula works for all percentage calculations.
Q2: How do I convert a decimal to a percentage?
A2: Multiply the decimal by 100%. For example, 0.75 * 100% = 75%.
Q3: How do I convert a fraction to a percentage?
A3: First, convert the fraction to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100%. For example, 3/4 = 0.75, and 0.75 * 100% = 75%.
Q4: What if my percentage calculation results in a decimal value?
A4: You can either leave the answer as a decimal percentage (e.g., 62.5%) or round it to the nearest whole number (e.g., 63%). The level of precision depends on the context of the problem.
Q5: Why are percentages important?
A5: Percentages are a universal and easily understandable way to represent proportions and comparisons. They're used across numerous fields, making data analysis and communication more effective.
Conclusion: Mastering Percentage Calculations
Understanding how to express 62 out of 100 as a percentage (which is 62%) is a fundamental step in mastering percentage calculations. This article has provided a detailed explanation of various methods and their applications in real-world scenarios. By mastering these concepts, you'll enhance your ability to analyze data, make informed decisions, and confidently tackle numerous mathematical problems in various fields of study and daily life. Remember to practice regularly and apply these techniques in different contexts to build a solid understanding of percentages. The more you practice, the more intuitive these calculations will become.
Latest Posts
Latest Posts
-
Convert 11 C To Fahrenheit
Sep 25, 2025
-
17 100 As A Percent
Sep 25, 2025
-
3 24 As A Percent
Sep 25, 2025
-
21 X What Equals 7
Sep 25, 2025
-
Gcf Of 35 And 15
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 62 100 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.