7/4 As A Mixed Number
horsecheck
Sep 24, 2025 · 6 min read
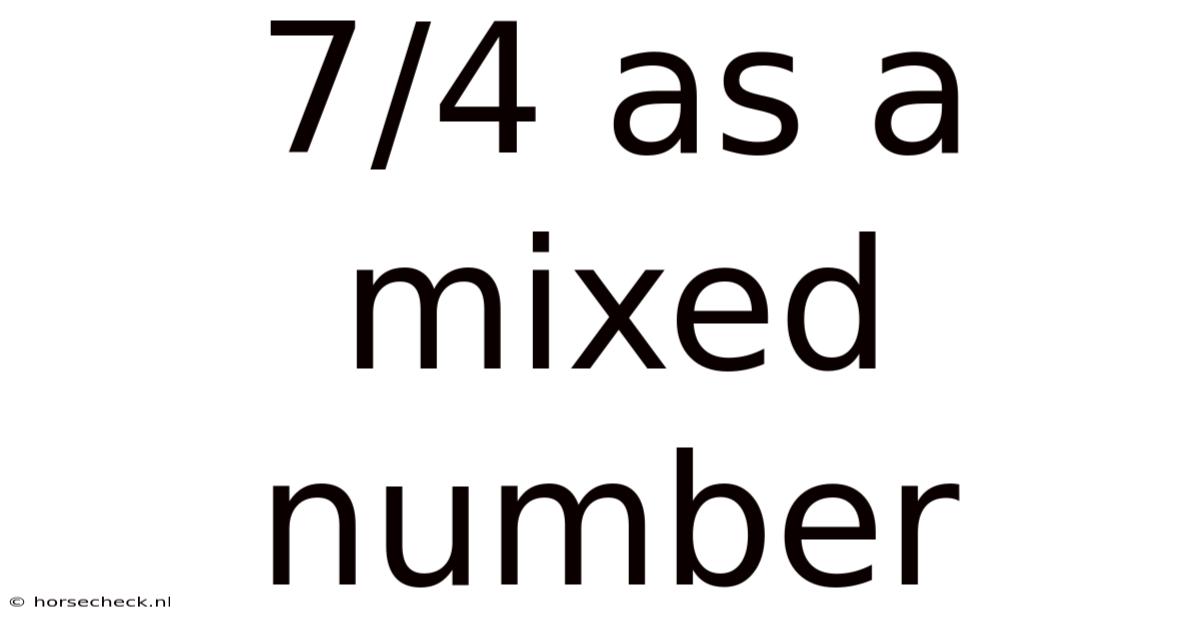
Table of Contents
Understanding 7/4 as a Mixed Number: A Comprehensive Guide
Fractions are a fundamental part of mathematics, forming the building blocks for more advanced concepts. Understanding how to represent fractions in different forms is crucial for success in math. This article provides a comprehensive guide to understanding the improper fraction 7/4 and how to convert it into its equivalent mixed number. We'll delve into the meaning of improper fractions and mixed numbers, explore the steps involved in the conversion process, and even touch upon the underlying mathematical principles. This guide is perfect for students learning about fractions, parents helping their children with homework, or anyone looking to refresh their understanding of this essential mathematical concept.
What are Improper Fractions and Mixed Numbers?
Before diving into the conversion of 7/4, let's establish a clear understanding of the terms involved.
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 9/5, and 12/12. The key characteristic is that the fraction represents a value greater than or equal to one.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers provide a more intuitive way to represent values greater than one. For example, 1 ¾ represents one whole unit and three-quarters of another unit.
The improper fraction 7/4 falls into the category of an improper fraction because the numerator (7) is greater than the denominator (4). Our goal is to convert this improper fraction into its equivalent mixed number representation.
Converting 7/4 to a Mixed Number: A Step-by-Step Guide
Converting an improper fraction to a mixed number involves a simple division process. Here's how to convert 7/4:
Step 1: Divide the Numerator by the Denominator
Divide the numerator (7) by the denominator (4).
7 ÷ 4 = 1 with a remainder of 3
Step 2: Identify the Whole Number and the Remainder
The result of the division gives us two important pieces of information:
- The quotient (1): This becomes the whole number part of the mixed number.
- The remainder (3): This becomes the numerator of the fractional part of the mixed number.
Step 3: Construct the Mixed Number
The denominator of the fractional part remains the same as the original denominator (4). Therefore, the mixed number equivalent of 7/4 is:
1 ³⁄₄
This means that 7/4 represents one whole unit and three-quarters of another unit.
Visualizing the Conversion: A Pictorial Representation
Imagine you have 7 identical pizzas, each cut into 4 equal slices. The fraction 7/4 represents having 7 of these slices.
To visualize the conversion to a mixed number, we group the slices into sets of 4 (since our denominator is 4). We can form one complete pizza (4 slices) and have 3 slices remaining. This corresponds perfectly to the mixed number 1 ³⁄₄.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the fundamental principle of representing quantities in different but equivalent forms. It utilizes the concept of division and remainders to express a value greater than one as a combination of a whole number and a fractional part.
The equation can be expressed as:
Improper Fraction = (Quotient * Denominator) + Remainder / Denominator = Mixed Number
In our example:
7/4 = (1 * 4) + 3 / 4 = 1 ³⁄₄
Further Examples and Practice
Let's practice converting a few more improper fractions into mixed numbers to solidify our understanding:
- 11/3: 11 ÷ 3 = 3 with a remainder of 2. Therefore, 11/3 = 3 ²⁄₃
- 17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ²⁄₅
- 23/6: 23 ÷ 6 = 3 with a remainder of 5. Therefore, 23/6 = 3 ⁵⁄₆
- 10/10: 10 ÷ 10 = 1 with a remainder of 0. Therefore, 10/10 = 1 (This is a special case where the improper fraction simplifies to a whole number)
These examples demonstrate the consistency of the method regardless of the specific numbers involved.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to be able to convert a mixed number back into its improper fraction equivalent. This involves reversing the process. Let's convert 1 ³⁄₄ back to an improper fraction:
Step 1: Multiply the Whole Number by the Denominator:
1 * 4 = 4
Step 2: Add the Numerator:
4 + 3 = 7
Step 3: Place the Result over the Original Denominator:
7/4
This confirms that the conversion between 7/4 and 1 ³⁄₄ is accurate.
Real-World Applications of Improper Fractions and Mixed Numbers
Understanding improper fractions and mixed numbers has practical applications in various real-world scenarios:
- Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities (e.g., 1 ½ cups of flour).
- Measurement: Measuring lengths, weights, and volumes frequently involves mixed numbers (e.g., 2 ¾ inches).
- Construction and Engineering: Precision in construction and engineering often requires working with fractional measurements, including mixed numbers.
- Data Analysis: When dealing with averages or other statistical measures, you may encounter mixed numbers representing the results.
The ability to easily convert between improper fractions and mixed numbers ensures accuracy and efficiency in these situations.
Frequently Asked Questions (FAQ)
Q: Why is it important to learn how to convert improper fractions to mixed numbers?
A: Converting between these forms is crucial for understanding and working with fractions more effectively. Mixed numbers are often easier to visualize and interpret in everyday contexts.
Q: Can every improper fraction be converted into a mixed number?
A: Yes, every improper fraction can be converted into either a mixed number or a whole number. If the remainder is zero after dividing the numerator by the denominator, then the result will be a whole number.
Q: What if the remainder is zero when converting an improper fraction?
A: If the remainder is zero, the improper fraction simplifies to a whole number. For instance, 8/4 simplifies to 2 because 8 divided by 4 equals 2 with a remainder of 0.
Q: Is there only one way to represent a given quantity as a fraction?
A: No, a given quantity can be represented by many equivalent fractions (e.g., ½ = 2/4 = 3/6...). However, there's only one unique representation as a mixed number in its simplest form.
Q: Are there any online tools or calculators to help with these conversions?
A: Yes, many online resources offer calculators that can convert improper fractions to mixed numbers and vice versa. However, understanding the underlying process is crucial for developing mathematical fluency.
Conclusion
Converting the improper fraction 7/4 to the mixed number 1 ³⁄₄ is a fundamental skill in mathematics. This article provided a comprehensive step-by-step guide, accompanied by visual representations and real-world applications. Understanding this conversion process not only helps in solving mathematical problems but also enhances numerical comprehension and problem-solving skills in various practical situations. Mastering this concept lays a solid foundation for future mathematical learning and applications. Remember to practice regularly, and you'll soon find yourself confident in handling fractions in all their forms.
Latest Posts
Latest Posts
-
Whats Xv In Roman Numerals
Sep 24, 2025
-
101 Degrees Fahrenheit In Celsius
Sep 24, 2025
-
Whats 0 3 As A Fraction
Sep 24, 2025
-
Simplest Form Of 4 5
Sep 24, 2025
-
Percent Of 4 Is 7
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.