What Is 1/5 Of 11
horsecheck
Sep 23, 2025 · 6 min read
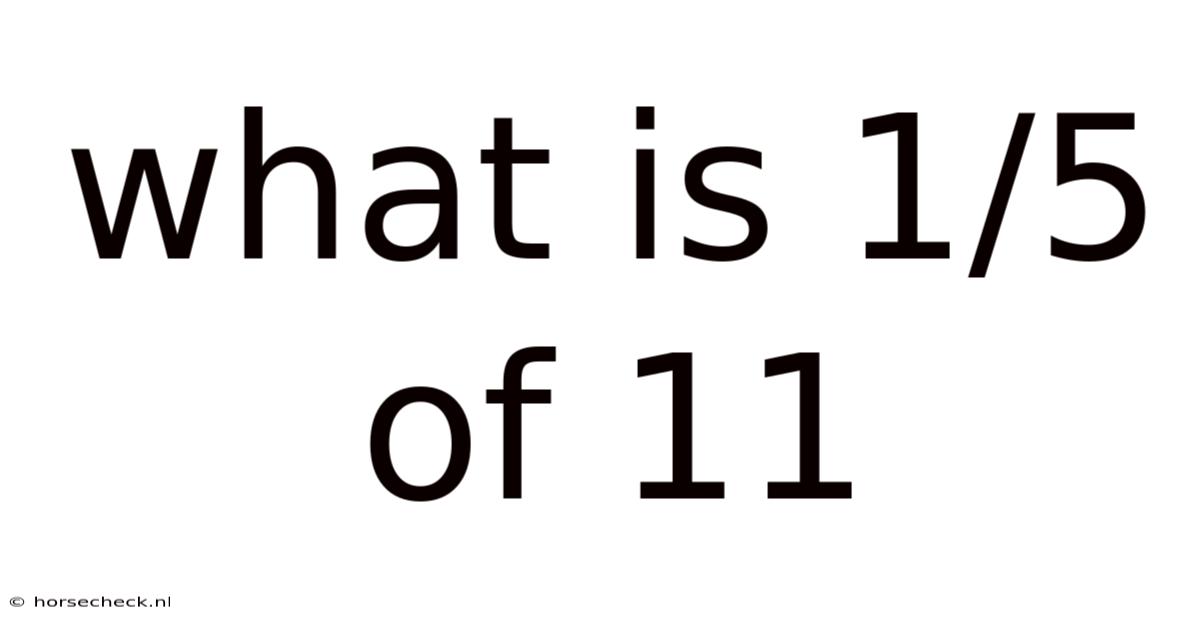
Table of Contents
What is 1/5 of 11? A Deep Dive into Fractions and Their Applications
Finding 1/5 of 11 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic equation unlocks a deeper understanding of fractions, their representation, and their extensive applications in various fields, from everyday life to complex scientific calculations. This article will not only answer the question "What is 1/5 of 11?" but also delve into the underlying mathematical concepts and explore practical examples to solidify your understanding.
Understanding Fractions: A Foundation
Before we tackle the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/5, the denominator (5) means the whole is divided into five equal parts, and the numerator (1) indicates we're taking one of those parts.
Calculating 1/5 of 11: The Step-by-Step Approach
To find 1/5 of 11, we need to perform a multiplication operation. We can express this as:
(1/5) * 11
There are several ways to approach this calculation:
Method 1: Direct Multiplication
We can directly multiply the fraction by the whole number:
(1/5) * 11 = 11/5
This gives us an improper fraction, meaning the numerator is larger than the denominator. To express this as a mixed number (a whole number and a fraction), we perform division:
11 ÷ 5 = 2 with a remainder of 1
Therefore, 11/5 is equal to 2 1/5.
Method 2: Converting to Decimal
We can convert the fraction 1/5 to its decimal equivalent:
1/5 = 0.2
Then, multiply the decimal by 11:
0.2 * 11 = 2.2
This gives us the same result as Method 1, just expressed as a decimal.
Method 3: Finding a Fraction of a Whole Number Intuitively
Imagine you have 11 pizzas. You want to find out how much pizza you get if you take 1/5 of them. You would divide the 11 pizzas into 5 equal groups. Each group represents 1/5 of the total pizzas.
11 pizzas ÷ 5 groups = 2.2 pizzas per group.
Each group contains 2 full pizzas and 0.2 of a pizza (or 1/5 of a pizza). Therefore, 1/5 of 11 is 2.2 or 2 1/5.
Visual Representation of the Problem
A visual representation can greatly aid in understanding this concept. Imagine a pizza cut into five equal slices. Each slice represents 1/5 of the whole pizza. If you have 11 such pizzas, finding 1/5 of them would mean taking one slice from each pizza. You would end up with 11 slices, which is equivalent to 2 whole pizzas and 1 slice (1/5 of a pizza).
Expanding the Concept: Fractions in Real-World Applications
The seemingly simple calculation of 1/5 of 11 has wide-ranging applications across diverse fields:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. For instance, a recipe might call for 1/5 of a cup of sugar. Understanding fractions is crucial for accurate measurement and consistent results.
-
Finance: Fractions are fundamental in financial calculations. Determining interest rates, calculating proportions of investments, or understanding stock market fluctuations all involve working with fractions.
-
Engineering and Construction: In engineering and construction, precise measurements are critical. Fractions are used in blueprints, calculations for material quantities, and ensuring the structural integrity of buildings.
-
Science and Medicine: Scientific experiments and medical dosages often require precise measurements, often expressed as fractions or decimals. Accurate calculations are essential for reliable results and patient safety.
-
Data Analysis: In statistics and data analysis, fractions and percentages are used to represent proportions and trends within datasets. Understanding fractional representations is crucial for interpreting data accurately.
-
Everyday Life: Sharing items fairly, calculating discounts, understanding sales, or determining the appropriate portion sizes for meals all involve working with fractions, even if subconsciously.
Beyond the Basics: Advanced Fraction Concepts
Understanding the calculation of 1/5 of 11 serves as a springboard to more complex fractional concepts:
-
Equivalent Fractions: Different fractions can represent the same value. For example, 1/5, 2/10, and 3/15 are all equivalent fractions. Understanding equivalent fractions is crucial for simplifying calculations and comparing fractions.
-
Adding and Subtracting Fractions: To add or subtract fractions, you need a common denominator. This involves finding a common multiple of the denominators of the fractions being added or subtracted.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions involves inverting the second fraction (reciprocal) and multiplying.
-
Fractions and Decimals: Fractions and decimals are interchangeable representations of the same value. Understanding how to convert between fractions and decimals is essential for flexibility in calculations.
-
Percentages: Percentages are simply fractions expressed as a proportion of 100. For example, 1/5 is equivalent to 20%.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to directly calculate (1/5) * 11. However, understanding the manual calculation process is crucial for developing a deeper understanding of fractions.
-
Q: What if the numbers were larger or more complex?
A: The same principles apply regardless of the size or complexity of the numbers. The core concept remains the same: multiplication of the fraction by the whole number.
-
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to many areas of mathematics and have numerous practical applications in everyday life, making their understanding crucial for navigating various aspects of life and work.
-
Q: Are there different ways to represent the answer 2 1/5?
A: Yes, the answer can be represented as a mixed number (2 1/5), an improper fraction (11/5), or a decimal (2.2). The preferred representation depends on the context and the desired level of precision.
Conclusion: Mastering Fractions for a Brighter Future
Finding 1/5 of 11, while seemingly simple, opens the door to a comprehensive understanding of fractions and their vast applications. Mastering fractional calculations is not just about solving arithmetic problems; it's about developing critical thinking skills, problem-solving abilities, and a foundational understanding of mathematics that is applicable across numerous fields. By understanding the underlying concepts and practicing regularly, you can build a strong foundation in mathematics and unlock a world of opportunities. Remember, even the most complex mathematical concepts are built upon fundamental principles, like understanding what 1/5 of 11 truly represents.
Latest Posts
Latest Posts
-
45 Degrees C In F
Sep 23, 2025
-
79 8 As A Mixed Number
Sep 23, 2025
-
2 7 8 As Decimal
Sep 23, 2025
-
Lcm Of 4 And 16
Sep 23, 2025
-
What Is 2 3 Of 60
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/5 Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.