What Times What Makes 81
horsecheck
Sep 23, 2025 · 5 min read
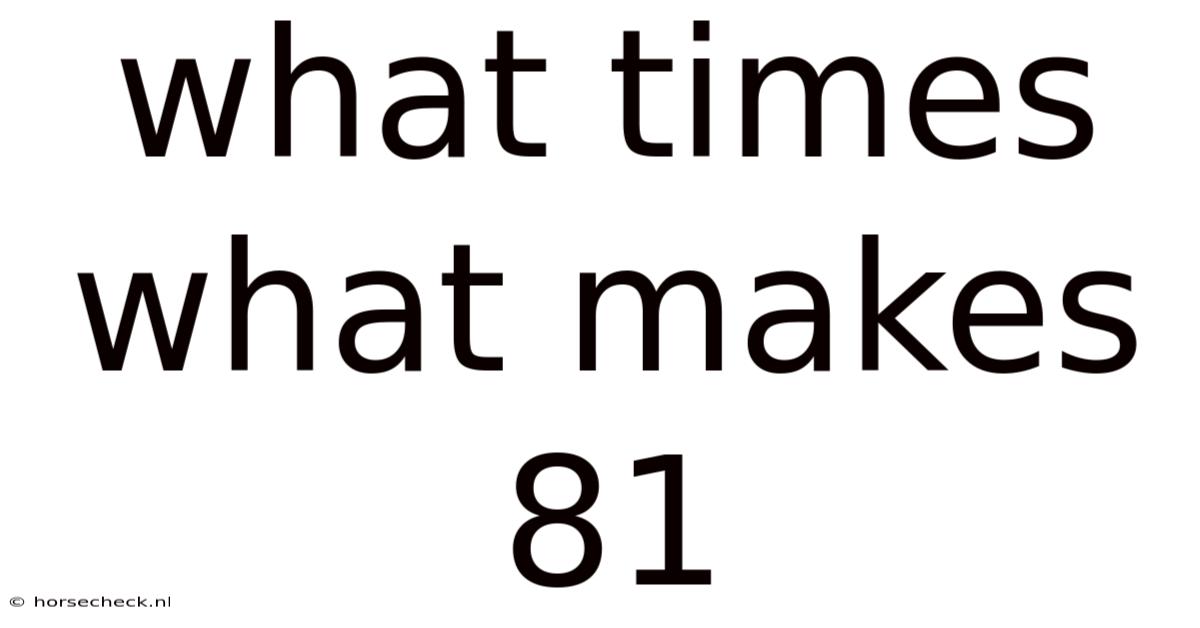
Table of Contents
What Times What Makes 81? Exploring Factors and Prime Factorization
Finding the factors of a number, like discovering what numbers multiplied together equal 81, is a fundamental concept in mathematics. This seemingly simple question opens the door to a deeper understanding of number theory, including prime factorization and the properties of integers. This comprehensive guide will not only answer the question "What times what makes 81?" but also delve into the underlying mathematical principles, offering insights valuable for students of all levels.
Understanding Factors and Multiples
Before diving into the specifics of 81, let's clarify the key terms. A factor of a number is a whole number that divides exactly into that number without leaving a remainder. Conversely, a multiple of a number is the result of multiplying that number by another whole number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides evenly into 12. Multiples of 12 include 12, 24, 36, 48, and so on.
Finding the Factors of 81: A Systematic Approach
The simplest way to find the factors of 81 is to systematically test each whole number. We can start by checking if 1 is a factor (it always is), then move on to 2, 3, and so forth.
- 1 x 81 = 81
- 3 x 27 = 81
- 9 x 9 = 81
- 27 x 3 = 81
- 81 x 1 = 81
Therefore, the factors of 81 are 1, 3, 9, 27, and 81. Notice that the factors appear in pairs, except for 9, which is multiplied by itself. This highlights an important property: perfect squares have an odd number of factors.
Prime Factorization: The Building Blocks of Numbers
Prime factorization is the process of expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization provides a unique representation of any composite number (a number that is not prime).
To find the prime factorization of 81, we can use a factor tree:
81
/ \
9 9
/ \ / \
3 3 3 3
This shows that 81 can be expressed as 3 x 3 x 3 x 3, or 3⁴. This is the prime factorization of 81. This means that 81 is a perfect fourth power of 3. Understanding prime factorization is crucial in various mathematical applications, including simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM).
Applications of Factors and Prime Factorization
The seemingly simple task of finding what numbers multiply to make 81 has broader applications across several mathematical concepts:
-
Simplifying Fractions: If you encounter a fraction with 81 in the numerator or denominator, knowing its factors allows you to simplify the fraction to its lowest terms. For example, 81/27 can be simplified to 3/1 (or simply 3) by dividing both numerator and denominator by their common factor, 27.
-
Solving Equations: Factors are essential in solving algebraic equations. For instance, solving the quadratic equation x² - 81 = 0 involves factoring the left-hand side as (x - 9)(x + 9) = 0, leading to solutions x = 9 and x = -9.
-
Number Theory: Prime factorization is fundamental in number theory, which explores the properties of integers. Concepts like modular arithmetic, cryptography, and the distribution of prime numbers rely heavily on prime factorization.
-
Geometry: Understanding factors can be helpful in solving geometric problems involving areas and volumes. For example, if the area of a square is 81 square units, the length of its side is the square root of 81, which is 9 units.
-
Real-World Applications: From dividing resources fairly (e.g., sharing 81 candies among friends) to optimizing layouts (e.g., arranging 81 tiles in a square pattern), understanding factors has practical applications in everyday life.
Beyond 81: Exploring Other Numbers
The approach to finding factors and prime factorization can be extended to any number. Let’s look at a few examples:
-
The Number 100: The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100. Its prime factorization is 2² x 5².
-
The Number 144: The factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144. Its prime factorization is 2⁴ x 3².
-
The Number 256: The factors of 256 are 1, 2, 4, 8, 16, 32, 64, 128, and 256. Its prime factorization is 2⁸.
By understanding the methods used for 81, you can easily adapt them to find the factors and prime factorization of any other number.
Frequently Asked Questions (FAQ)
Q: What is the square root of 81?
A: The square root of 81 is 9, because 9 x 9 = 81.
Q: Is 81 a prime number?
A: No, 81 is not a prime number. It is a composite number because it has more than two factors.
Q: How many factors does 81 have?
A: 81 has five factors: 1, 3, 9, 27, and 81.
Q: What are some real-world examples where understanding factors of 81 could be useful?
A: Imagine you need to arrange 81 chairs in a square formation for an event. Knowing that 9 x 9 = 81 helps you determine the number of chairs needed per side. Or, if you have 81 cookies to distribute evenly amongst several groups, understanding the factors helps you determine how many groups you can make with equal sharing.
Conclusion: Unlocking the Power of Number Theory
The seemingly simple question "What times what makes 81?" opens a gateway to a richer understanding of fundamental mathematical concepts. By exploring factors, prime factorization, and their applications, we discover the building blocks of numbers and their interconnectedness. This knowledge isn't just about solving equations; it empowers us to approach various mathematical and real-world problems with greater confidence and efficiency. The journey into number theory, starting with a simple multiplication problem like this, is an exciting exploration that reveals the elegance and power of mathematics. Remember, even seemingly basic arithmetic operations can hold profound mathematical significance when explored deeply.
Latest Posts
Latest Posts
-
85 Degrees F To Celcius
Sep 23, 2025
-
What Is 8 Of 60
Sep 23, 2025
-
What Is 1 7 2
Sep 23, 2025
-
41 Grados Celsius A Fahrenheit
Sep 23, 2025
-
What Is 20 Of 9
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Times What Makes 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.